摘要：已知三棱锥S-ABC的三条侧棱SA.SB.SC两两互相垂直且长度分别为a.b.c.设O为S在底面ABC上的射影.求证: (1)O为△ABC的垂心, (2)O在△ABC内, (3)设SO=h.则 + +=. 证明:(1)∵SA⊥SB.SA⊥SC. ∴SA⊥平面SBC.BC平面SBC.∴SA⊥BC. 而AD是SA在平面ABC上的射影.∴AD⊥BC. 同理可证AB⊥CF.AC⊥BE.故O为△ABC的垂心. (2)证明△ABC为锐角三角形即可.不妨设a≥b≥c.则底面三角形ABC中.AB=为最大.从而∠ACB为最大角. 用余弦定理求得:cos∠ACB=>0. ∴∠ACB为锐角.△ABC为锐角三角形.故O在△ABC内. (3)SB·SC=BC·SD. 故SD=.= +. 又SA·SD=AD·SO. == = += ++=.
网址：http://m.1010jiajiao.com/timu_id_3975897[举报]
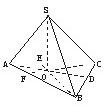已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c，设O为S在底面ABC上的射影．求证：（1）O为△ABC的垂心；
（2）O在△ABC内；
（3）设SO=h，则
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| h2 |
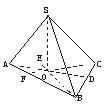已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c，设O为S在底面ABC上的射影．
求证：（1）O为△ABC的垂心；
（2）O在△ABC内；
（3）设SO=h，则
+
+
=
．
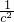查看习题详情和答案>>
已知三棱锥S—ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c,设O为S在底面ABC上的射影.求证:
(1)O为△ABC的垂心;
(2)O在△ABC内;
(3)设SO=h,则
+
+
=
.
+
+
=
．