摘要:球的概念和性质以及面积.体积是解决有关问题的重要依据,它的轴截面是解决问题的重要“场所 .球半径.截面圆半径.圆心距都在这个图形内.它把空间问题转化为平面问题.
网址:http://m.1010jiajiao.com/timu_id_3975887[举报]
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),GM∥AB.
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
•
=-2?若存在,求出直线l的方程,若不存在,说明理由.
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
=
=
=
.
查看习题详情和答案>>
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
| OP |
| OQ |
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),GM∥AB.
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
•
=-2?若存在,求出直线l的方程,若不存在,说明理由.
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
=
=
=
.
查看习题详情和答案>>
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线E,是否存在直线l,使l过点(0.1)并与曲线E交于P、Q两点,且满足
| OP |
| OQ |
注:三角形的重心的概念和性质如下:设△ABC的重心,且有
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
 已知某几何体是一个圆柱和一个球的组合体,球的直径和
已知某几何体是一个圆柱和一个球的组合体,球的直径和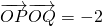 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.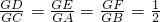 .
. A.
A.