摘要：∵. ∴四边形DBFE是平行四边形 ∴ DE=BF, ∵ 是的中点． ∴BF=CF ∴ 证明:∵DE∥BC,EF∥AB, ∴四边形BDEF是平行四边形 ∴DE=BF ∵F是BC的中点 ∴BF=CF ∴DE=CF
网址：http://m.1010jiajiao.com/timu_id_3973787[举报]
如图，△ABC是由四个全等的三角形△ADE、△DBF、△FED、△EFC拼接而成，则图中的平行四边形有已知A（-1，0），B（0，-3），点C与点A关于坐标原点对称，经过点C的直线与y轴交于点D，与直线AB交于点E．
（1）若点D（ 0，1），过点B作BF⊥CD于F，求∠DBF的度数及四边形ABFD的面积；
（2）若点G（G不与C重合）是动直线CD上一点，点D在点（0，1）的上方，且BG=BA，试探究∠ABG与∠ECA之间的等量关系．
查看习题详情和答案>>
（1）若点D（ 0，1），过点B作BF⊥CD于F，求∠DBF的度数及四边形ABFD的面积；
（2）若点G（G不与C重合）是动直线CD上一点，点D在点（0，1）的上方，且BG=BA，试探究∠ABG与∠ECA之间的等量关系．
在平面内，旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度而得到新位置图形的一种变换．
活动一：如图1，在Rt△ABC中，D为斜边AB上的一点，AD=2，BD=1，且四边形DECF是正方形，求阴影部分的面积．
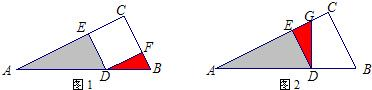
小明运用图形旋转的方法，将△DBF绕点D逆时针旋转90°，得到△DGE（如图2所示），一眼就看出这题的答案，请你写出阴影部分的面积： ．
活动二：如图3，在四边形ABCD中，AB=AD，∠BAD=∠C=90°，BC=5，CD=3，过点A作AE⊥BC，垂足为点E，求AE的长．
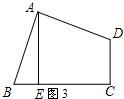
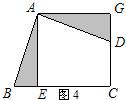
小明仍运用图形旋转的方法，将△ABE绕点A逆时针旋转90°，得到△ADG（如图4所示），则①四边形AECG是怎样的特殊四边形？答： ．AE的长是 ．
活动三：如图5，在四边形ABCD中，AB⊥AD，CD⊥AD，将BC按逆时针方向绕点B旋转90°得到线段BE，连接AE．若AB=2，DC=4，求△ABE的面积．
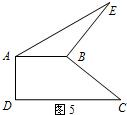查看习题详情和答案>>
活动一：如图1，在Rt△ABC中，D为斜边AB上的一点，AD=2，BD=1，且四边形DECF是正方形，求阴影部分的面积．
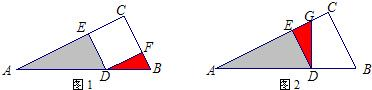
小明运用图形旋转的方法，将△DBF绕点D逆时针旋转90°，得到△DGE（如图2所示），一眼就看出这题的答案，请你写出阴影部分的面积：
活动二：如图3，在四边形ABCD中，AB=AD，∠BAD=∠C=90°，BC=5，CD=3，过点A作AE⊥BC，垂足为点E，求AE的长．
小明仍运用图形旋转的方法，将△ABE绕点A逆时针旋转90°，得到△ADG（如图4所示），则①四边形AECG是怎样的特殊四边形？答：
活动三：如图5，在四边形ABCD中，AB⊥AD，CD⊥AD，将BC按逆时针方向绕点B旋转90°得到线段BE，连接AE．若AB=2，DC=4，求△ABE的面积．
查看习题详情和答案>>
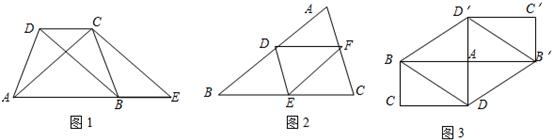
如果存在，直接写出最大值、最小值；如果不存在，请说明理由．