题目内容
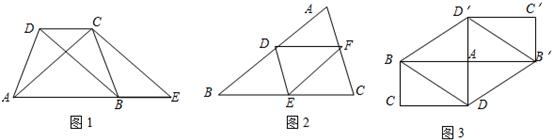
如图，△ABC是由四个全等的三角形△ADE、△DBF、△FED、△EFC拼接而成，则图中的平行四边形有3
3
个．分析：根据全等三角形的性质可得AD=EF，AE=DF，DB=EF，DE=BF，DE=FC，DF=EC，根据两组对边分别相等的四边形是平行四边形可得答案．
解答：解：∵△ADE、△FED是全等的三角形，
∴AD=EF，AE=DF，
∴四边形ADFE是平行四边形，
∵△DBF、△FED是全等的三角形，
∴DB=EF，DE=BF，
∴四边形DBFE是平行四边形，
∵△EFC、△FED是全等的三角形，
∴DE=FC，DF=EC，
∴四边形DFCE是平行四边形，
故答案为：3．
∴AD=EF，AE=DF，
∴四边形ADFE是平行四边形，
∵△DBF、△FED是全等的三角形，
∴DB=EF，DE=BF，
∴四边形DBFE是平行四边形，
∵△EFC、△FED是全等的三角形，
∴DE=FC，DF=EC，
∴四边形DFCE是平行四边形，
故答案为：3．
点评：此题主要考查了全等三角形的性质，以及平行四边形的判定，关键是掌握两组对边分别相等的四边形是平行四边形．
练习册系列答案
小学教材完全解读系列答案
相关题目
如图，是由四个边长为1的小正方形拼成的一个大正方形，连接A，B，C点得到△ABC．
