摘要：11．已知直线l的参数方程:(t为参数)和圆C的极坐标方程:ρ＝2sin(θ+)(θ为参数)． (1)将直线l的参数方程和圆C的极坐标方程化为直角坐标方程, (2)判断直线l和圆C的位置关系． 解:(1)消去参数t.得直线l的直角坐标方程为y＝2x+1, ρ＝2sin(θ+)即ρ＝2(sinθ+cosθ). 两边同乘以ρ得ρ2＝2(ρsinθ+ρcosθ). 消去参数θ.得⊙C的直角坐标方程为: (x-1)2+(y-1)2＝2. (2)圆心C到直线l的距离 d＝＝＜. 所以直线l和⊙C相交．
网址：http://m.1010jiajiao.com/timu_id_3971635[举报]
已知直线l的参数方程：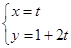
(t为参数)和圆C的极坐标方程：ρ＝2
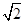sin(θ＋
)．
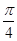(1)将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
(2)判断直线l和圆C的位置关系．
查看习题详情和答案>>
已知直线l的参数方程：
(t为参数)和圆C的极坐标方程：ρ＝2
sin(θ＋
)．
(1)将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
(2)判断直线l和圆C的位置关系．
已知直线l的参数方程：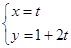
(t为参数)和圆C的极坐标方程：ρ＝2
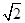sin(θ＋
)．
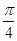(1)将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
(2)判断直线l和圆C的位置关系．
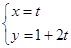(t为参数)和圆C的极坐标方程：ρ＝2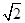sin(θ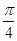＋)．(1)将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
(2)判断直线l和圆C的位置关系．
(t为参数)和圆C的极坐标方程：ρ＝2
sin(
＋
)
(t为参数)和圆C的极坐标方程：
．