摘要:11.△ABC的三个内角A.B.C成等差数列.a.b.c分别为三内角A.B.C的对边.求证:+=. 证明:要证明+=. 只需证明+=3. 只需证明+=1. 只需证明c(b+c)+a(a+b)=(a+b)·(b+c). 只需证明c2+a2=ac+b2. ∵△ABC的三个内角A.B.C成等差数列.∴B=60°. 由余弦定理.有b2=c2+a2-2accos60°. 即b2=c2+a2-ac. ∴c2+a2=ac+b2.故原命题成立.得证.
网址:http://m.1010jiajiao.com/timu_id_3971623[举报]
 求证:
求证: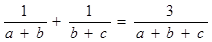
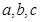 分别为三个内角A、B、C所对的边,
分别为三个内角A、B、C所对的边,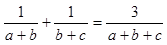 。 (13分)
。 (13分)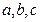 分别为三个内角A、B、C所对的边,
分别为三个内角A、B、C所对的边,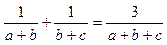 。 (13分)
。 (13分)