摘要：已知数列{an}的每一项都是正数.满足a1＝2且a-anan+1-2a＝0,等差数列{bn}的前n项和为Tn.b2＝3.T5＝25. (1)求数列{an}.{bn}的通项公式, (2)比较++-+与2的大小, (3)若++-+＜c恒成立.求整数c的最小值. 解:(1)由a-anan+1-2a＝0. 得(an+1-2an)(an+1+an)＝0. 由于数列{an}的每一项都是正数.∴an+1＝2an.∴an＝2n. 设bn＝b1+(n-1)d.由已知有b1+d＝3,5b1+d＝25. 解得b1＝1.d＝2.∴bn＝2n-1. 得Tn＝n2.∴＝. 当n＝1时.＝1＜2. 当n≥2时.＜＝-. ∴++-+＜1+-+-+-+-＝2-＜2. (3)记Pn＝++-+＝+++-+. ∴Pn＝++-++. 两式相减得Pn＝3-. ∵Pn递增.∴≤Pn＜3.P4＝＞2. ∴最小的整数c＝3.
网址：http://m.1010jiajiao.com/timu_id_3971499[举报]
已知数列{an}的每一项都是正数，满足a1=2，且an+12-anan+1-2an2=0；等差数列{bn}的前n项和为Tn，b2=3，T5=25．
（1）求数列{an}、{bn}的通项公式；
（2）比较
+
+…+
与2的大小；
（3）若
+
+…+
＜c恒成立，求整数c的最小值．
查看习题详情和答案>>
（1）求数列{an}、{bn}的通项公式；
（2）比较
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
（3）若
| b1 |
| a1 |
| b2 |
| a2 |
| bn |
| an |
已知数列{an}的每一项都是正数，满足a1=2，且an+12-anan+1-2an2=0；等差数列{bn}的前n项和为Tn，b2=3，T5=25．
（1）求数列{an}、{bn}的通项公式；
（2）比较
+
+…+
与2的大小；
（3）若
+
+…+
＜c恒成立，求整数c的最小值．
查看习题详情和答案>>
（1）求数列{an}、{bn}的通项公式；
（2）比较
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
（3）若
| b1 |
| a1 |
| b2 |
| a2 |
| bn |
| an |
已知数列{an}的每一项都是正数，满足a1=2，且an+12-anan+1-2an2=0；等差数列{bn}的前n项和为Tn，b2=3，T5=25．
（1）求数列{an}、{bn}的通项公式；
（2）比较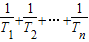
与2的大小；
（3）若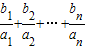
＜c恒成立，求整数c的最小值．
查看习题详情和答案>>
（1）求数列{an}、{bn}的通项公式；
（2）比较
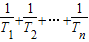与2的大小；（3）若
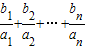＜c恒成立，求整数c的最小值．查看习题详情和答案>>
已知数列{an}的每一项都是正数，满足a1=2，且an+12-anan+1-2an2=0；等差数列{bn}的前n项和为Tn，b2=3，T5=25．
（1）求数列{an}、{bn}的通项公式；
（2）比较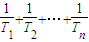
与2的大小；
（3）若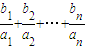
＜c恒成立，求整数c的最小值．
查看习题详情和答案>>
（1）求数列{an}、{bn}的通项公式；
（2）比较
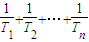与2的大小；（3）若
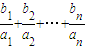＜c恒成立，求整数c的最小值．查看习题详情和答案>>
已知数列{an}的首项a1＝1，a2＝3，前n项和为Sn，且
，(n∈N*，n≥2)，数列{bn}满足b1＝1，bn+1＝log2(an＋1)＋bn
(Ⅰ)判断数列{an＋1}是否为等比数列，并证明你的结论；
(Ⅱ)设
，求c1＋c2＋c3……＋cn；
(Ⅲ)对于(Ⅰ)中数列{an}，若数列{In}满足ln＝log2(an＋1)(n∈N*)，在每两个lk与lk+1之间都插入2k－1(k＝1，2，3，…k∈N*)个2，使得数列{ln}变成了一个新的数列{tp}，(p∈N*)试问：是否存在正整数m，使得数列{tp}的前m项的和Tm＝2011？如果存在，求出m的值；如果不存在，说明理由．