摘要: 如图.PA垂直于矩形ABCD所在的平面.AD=PA=2.CD=2.E.F分别是AB.PD的中点. (1)求证:AF∥平面PCE, (2)求证:平面PCE⊥平面PCD, (3)求四面体PEFC的体积. 解:(1)证明:设G为PC的中点.连结FG.EG. ∵F为PD的中点.E为AB的中点. ∴FG CD.AECD ∴FG AE.∴AF∥GE ∵GE⊂平面PEC. ∴AF∥平面PCE, (2)证明:∵PA=AD=2.∴AF⊥PD 又∵PA⊥平面ABCD.CD⊂平面ABCD. ∴PA⊥CD.∵AD⊥CD.PA∩AD=A. ∴CD⊥平面PAD. ∵AF⊂平面PAD.∴AF⊥CD. ∵PD∩CD=D.∴AF⊥平面PCD. ∴GE⊥平面PCD. ∵GE⊂平面PEC. ∴平面PCE⊥平面PCD, 知.GE⊥平面PCD. 所以EG为四面体PEFC的高. 又GF∥CD.所以GF⊥PD. EG=AF=.GF=CD=. S△PCF=PD·GF=2. 得四面体PEFC的体积V=S△PCF·EG=.
网址:http://m.1010jiajiao.com/timu_id_3971413[举报]
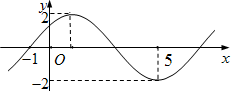 (2010•徐州模拟)若函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则ω的值为
(2010•徐州模拟)若函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则ω的值为