摘要:如图.AD⊥平面BCD.∠BCD=90°.AD=BC=CD=a.则二面角 C-AB-D的大小为 . 解析:取BD的中点E.连结CE.则CE⊥面ABD.作EF⊥AB. ∴CF⊥AB得∠CFE为所求. 又CE=a.CF=. ∴sin∠CFE= 答案:60°
网址:http://m.1010jiajiao.com/timu_id_3971408[举报]
如图,已知∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且![]() =
=![]() =λ.
=λ.
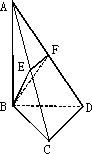
(1)求证:平面BEF⊥平面ABC.
(2)当λ为何值时,平面BEF⊥平面ACD.
如图,已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90°,PA=PB,PC=PD

(1)证明:平面PAB⊥平面ABCD;
(2)如果AD=1,BC=3,CD=4,且侧面PCD的面积为8,求四棱锥P-ABCD的体积.
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体A-BCD中,下列说法正确的是( )

A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABD
查看习题详情和答案>>
