摘要:定义在R上的函数f(x)满足f(x)=f(x+4).当2≤x≤6时.f(x)= ()|x-m|+n.f(4)=31. (1)求m.n的值, (2)比较f(log3m)与f(log3n)的大小. 解:(1)因为函数f(x)在R上满足f(x)=f(x+4). 所以4是函数f(x)的一个周期. 可得f(2)=f+n=()+n. ① 又f+n=31. ② 联立①②组成方程组解得m=4.n=30. 知.函数f(x)=()+30.x∈[2,6]. 因为1<log34<2.所以5<log34+4<6. f(log3m)=f(log34)=f(log34+4) =()+30 =()|log34|+30. 又因为3<log330<4.
网址:http://m.1010jiajiao.com/timu_id_3971247[举报]
(本小题满分13分)
已知定义在R上的函数![]() (a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值
(a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值![]() .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)证明:对任意![]() ∈[-1,1],不等式
∈[-1,1],不等式![]() 成立;
成立;
(Ⅲ)若函数![]() 在区间(1,∞)内无零点,求实数m的取值范围.
在区间(1,∞)内无零点,求实数m的取值范围.
 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时
时 ;
; -1有三个零点,求K的取值范围;
-1有三个零点,求K的取值范围;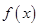 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时
时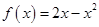 ;
;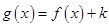 -1有三个零点,求K的取值范围;
-1有三个零点,求K的取值范围; 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时
时 ;
; -1有三个零点,求K的取值范围;
-1有三个零点,求K的取值范围;