摘要：如图.点A.B是单位圆上的两点.A.B点分别在第一 .二象限.点C是圆与x轴正半轴的交点.△AOB是正三角形.若点A的坐标 为(.).记∠COA＝α. (1)求的值, (2)求|BC|2的值. 解:(1)∵A的坐标为(.).根据三角函数的定义可知. sinα＝.cosα＝. ∴＝＝. (2)∵△AOB为正三角形.∴∠AOB＝60°. ∴cos∠COB＝cos(α+60°)＝cosαcos60°-sinαsin60° ＝×-×＝. ∴|BC|2＝|OC|2+|OB|2-2|OC|·|OB|cos∠COB ＝1+1-2×＝.
网址：http://m.1010jiajiao.com/timu_id_3971204[举报]
(本小题满分12分) 如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的一点．
（1）证明：平面PAC⊥平面PBC；
（2）若
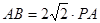，∠ABC=30°，求二面角A—PB—C的大小．
查看习题详情和答案>>
(本小题满分12分) 如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的一点．
（1）证明：平面PAC⊥平面PBC；
（2）若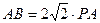
，∠ABC=30°，求二面角A—PB—C的大小．
（1）证明：平面PAC⊥平面PBC；
（2）若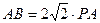，∠ABC=30°，求二面角A—PB—C的大小．(本小题满分12分)
如图，已知直平行六面体ABCD－A1B1C1D1中，AD⊥BD，AD=BD=a，E是CC1的中点，A1D⊥BE．
（I）求证：A1D⊥平面BDE；
（II）求二面角B―DE―C的大小；
如图，已知直平行六面体ABCD－A1B1C1D1中，AD⊥BD，AD=BD=a，E是CC1的中点，A1D⊥BE．
（I）求证：A1D⊥平面BDE；
（II）求二面角B―DE―C的大小；
a，AD
．
（1）求a的最大值；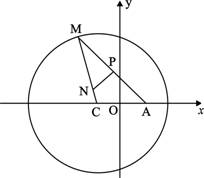
(本小题满分12分) 如图所示，已知圆
为圆上一动点，点
在
上，点
在
上，且满足
的轨迹为曲线
.
且斜率为k的动直线
交曲线
使四边
为矩形？若存在，求出G的坐标和四边形