Question

(本小题满分12分)

如图,四棱锥S-ABCD的底面是矩形，ABa，AD2，SA1，且SA⊥底面ABCD，若

边BC上存在异于B，C的一点P，使得．

（1）求a的最大值；

（2）当a取最大值时，求平面SCD的一个单位法向量

及点P到平面SCD的距离．

Answer 1

（本小题满分12分）

 解：建立如图所示的空间直角坐标系,则各点坐标分别为:

        A(0,0,0)，B(a,0,0)，C(a,2,0)，D(0,2,0)，S(0,0,1)，设P(a,x,0) (0<x<2)

      (1) ∵………2分

∴由得: ×=0,

即：     ………4分

∴当且仅当x=1时，a有最大值为1．

此时P为BC中点．                ………6分

      (2) 设是平面SCD的一个法向量， 由(1)知：

∴由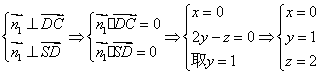得

∴平面SCD的一个单位法向量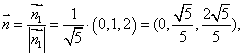

又在方向上的投影为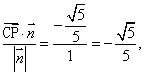

∴点P到平面SCD的距离为．                           ………12分