摘要：已知直角梯形ABCD中.AB∥CD.AB⊥BC.AB＝1.BC＝2.CD＝1+.过A作AE⊥CD.垂足为E.G.F分别为AD.CE的中点.现将△ADE沿AE折叠.使DE⊥EC. (1)求证:BC⊥平面CDE, (2)求证:FG∥平面BCD, (3)求四棱锥D-ABCE的体积. 解:(1)证明:由已知得: DE⊥AE.DE⊥EC.∴DE⊥平面ABCE. ∴DE⊥BC.又BC⊥CE.CE∩DE＝E. ∴BC⊥平面DCE. (2)证明:取AB中点H.连结GH.FH. ∴GH∥BD.FH∥BC. ∴GH∥平面BCD.FH∥平面BCD. 又GH∩FH＝H. ∴平面FHG∥平面BCD. ∴FG∥平面BCD. (3)V＝×1×2×＝.
网址：http://m.1010jiajiao.com/timu_id_3971181[举报]
（本小题满分12分）如图，已知四棱锥P―ABCD的底面是直角梯形，
，AB=BC=PB=PC=2CD=2，侧面
底面ABCD，
是BC中点，AO交BD于E.（I）求证：
；（II）求二面角
的大小；（III）求证：平面
平面PAB.
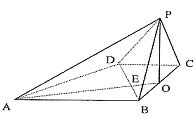
（本小题满分12分）
如图，已知四棱锥P—ABCD的底面是直角梯形，
，AB=BC=PB=PC=2CD=2，侧面
底面ABCD，O是BC中点，AO交BD于E.
（1）求证：
；
（2）求二面角
的大小；
（3）求证：平面
平面PAB.
（本小题满分12分）如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.
（1） 求异面直线AF与BG所成的角的大小；
（2） 求平面APB与平面CPD所成的锐二面角的大小.
查看习题详情和答案>>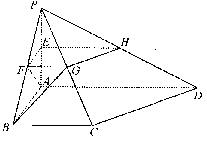
（本小题满分12分）如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.