题目内容
（本小题满分12分）
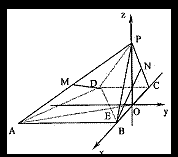
如图，已知四棱锥P—ABCD的底面是直角梯形，
，AB=BC=PB=PC=2CD=2，侧面
底面ABCD，O是BC中点，AO交BD于E.
（1）求证：
；
（2）求二面角
的大小；
（3）求证：平面
平面PAB.
…
解析:
方法一：（I）证明：
，又
平面
平面ABCD，平面
平面ABCD＝BC，
平面ABCD ……2分
在梯形ABCD中，可得
，即
在平面ABCD内的射影为AO，
……4分
（II）解：
，且平面平面ABCD
平面PBC， 
平面PBC，
为二面角P—DC—B的平面角 ……6分
是等边三角形
即二面角P—DC—B的大小为 …8分
（III）证明：取PB的中点N，连结CN，
①
，且平面平面ABCD，
平面PBC ……10分
平面PAB 
平面平面PAB ②
由①、②知
平面PAB…………..10分
连结DM、MN，则由MN//AB//CD，
，
得四边形MNCD为平行四边形，
，
平面PAB．
平面PAD 平面
平面PAB ……………….12分
方法二：取BC的中点O，因为
是等边三角形，
由侧面底面ABCD 得
底面ABCD ……1分
以BC中点O为原点，以BC所在直线为x轴，过点O与AB平行的直线为y轴，建立如图所示的空间直角坐标系O—xyz……2分
（I）证明：
，则在直角梯形中，
在等边三角形PBC中，
……3分
，即
…4分
（II）解：取PC中点N，则
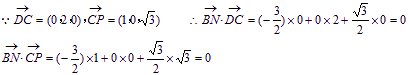
平面PDC，显然
，且
平面ABCD
所夹角等于所求二面角的平面角 ……6分
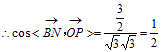，二面角
的大小为 ……8分
（III）证明：取PA的中点M，连结DM，则M的坐标为
又
……10分
，
即
平面PAB，平面平面PAB ……12分
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
