摘要： 异面直线.异面直线所成的角,两条异面直线互相垂直的概念,异面直线的公垂线及距离.
网址：http://m.1010jiajiao.com/timu_id_3966677[举报]
如图所示，已知两条异面直线AB与CD所成的角等于
，且AB＝m，CD＝n，平面MNPQ与AB、CD都平行，且M、N、P、Q依次在线段AC、BC、BD、AD上．
(1)求证：MNPQ是平行四边形；
(2)当M点在何位置时，
MNPQ的面积最大？最大面积是多少？
已知m、n是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列四个命题：
①若m⊥α，m⊥β，则α∥β；
②若α⊥γ，β⊥γ，则α∥β；
③若m∥n，且m与α，n与β所成的角相等，则α∥β；
④若m、n是异面直线，m?α，m∥β，n?β，n∥α，则α∥β，
其中真命题是（ ）
A．①和②
B．①和③
C．③和④
D．①和④
查看习题详情和答案>>
①若m⊥α，m⊥β，则α∥β；
②若α⊥γ，β⊥γ，则α∥β；
③若m∥n，且m与α，n与β所成的角相等，则α∥β；
④若m、n是异面直线，m?α，m∥β，n?β，n∥α，则α∥β，
其中真命题是（ ）
A．①和②
B．①和③
C．③和④
D．①和④
查看习题详情和答案>>
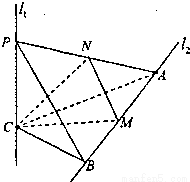
如图，l1，l2是两条互相垂直的异面直线，点P，C在直线l1上，点A， B在直线l2上，M，N分别是线段AB，AP的中点，且PC=AC=a，PA=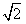
a，
(Ⅰ)证明：PC⊥平面ABC；
(Ⅱ)设平面MNC与平面PBC所成的角为θ(0°＜θ≤90°)。现给出下列四个条件：①CM=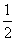
AB；②AB=
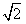a；③CM⊥AB；④BC⊥AC。请你从中再选择两个条件以确定cosθ的值，并求解．
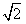a，(Ⅰ)证明：PC⊥平面ABC；
(Ⅱ)设平面MNC与平面PBC所成的角为θ(0°＜θ≤90°)。现给出下列四个条件：①CM=
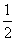AB；②AB=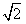a；③CM⊥AB；④BC⊥AC。请你从中再选择两个条件以确定cosθ的值，并求解．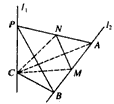 
．
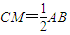；②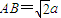
；③CM⊥AB；④BC⊥AC．
≤180°；
，0)对称．其中正确的是________(写出所有正确的序号)．