题目内容
如图所示,已知两条异面直线AB与CD所成的角等于 ,且AB=m,CD=n,平面MNPQ与AB、CD都平行,且M、N、P、Q依次在线段AC、BC、BD、AD上.
,且AB=m,CD=n,平面MNPQ与AB、CD都平行,且M、N、P、Q依次在线段AC、BC、BD、AD上.

(1)求证:MNPQ是平行四边形;
(2)当M点在何位置时, MNPQ的面积最大?最大面积是多少?
MNPQ的面积最大?最大面积是多少?
答案:
解析:
解析:
|
(1)由于AB∥平面MNPQ,平面ABC∩平面MNPQ=MN,则AB∥MN. 同理,AB∥PQ ∴MN∥PQ 同理MQ∥NP 故MNPQ是平行四边形. (2)由于AB与CD所成的角等于 设CM∶MA=λ∶1,则CM∶CA=λ∶(1+λ),AM∶AC=1∶(1+λ). 则MN=AB· ∴S = 其中当λ=1时,S |

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 ,AB∥MN,CD∥MQ,则sin∠NMQ=sin
,AB∥MN,CD∥MQ,则sin∠NMQ=sin ,MQ=CD·
,MQ=CD·
 MNPQ=MN·MQ·sin∠NMQ
MNPQ=MN·MQ·sin∠NMQ ≤
≤
 mnsin
mnsin (2006•静安区二模)如图所示,已知长方体ABCD-A1B1C1D1中,AC与BD交于E点,且AB=AD=2,两条异面直线A1D与AC所成的角的大小为
(2006•静安区二模)如图所示,已知长方体ABCD-A1B1C1D1中,AC与BD交于E点,且AB=AD=2,两条异面直线A1D与AC所成的角的大小为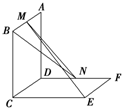 如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M、N分别为AB、DF的中点,求证:直线ME与BN是两条异面直线.
如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M、N分别为AB、DF的中点,求证:直线ME与BN是两条异面直线. 如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M, N分别为AB,DF的中点.
如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M, N分别为AB,DF的中点. 如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M, N分别为AB,DF的中点.
如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M, N分别为AB,DF的中点.