摘要:例1 如图.已知是平面的一条斜线.为斜足.为垂足.为内的一条直线..求斜线和平面所成角 解:∵.由斜线和平面所成角的定义可知.为和所成角. 又∵. ∴. ∴.即斜线和平面所成角为. 例2.如图.在正方体中.求面对角线与对角面所成的角 解法一:连结与交于.连结. ∵..∴平面. ∴是与对角面所成的角. 在中..∴. 解法二:由法一得是与对角面所成的角. 又∵.. ∴.∴. 说明:求直线与平面所成角的一般方法是先找斜线在平面中的射影.后求斜线与其射影的夹角另外.在条件允许的情况下.用公式求线面角显得更加方便 解法三:建立空间直角坐标系.用向量计算 例3.已知空间四边形的各边及对角线相等.求与平面所成角的余弦值 解:过作平面于点.连接. ∵.∴是正三角形的外心. 设四面体的边长为.则. ∵.∴即为与平面所成角. ∴.所以.与平面所成角的余弦值为. 例4 如图.已知AP⊥BP.PA⊥PC.∠ABP=∠ACP=60º.PB=PC=BC.D是BC中点.求AD与平面PBC所成角的余弦值. 解:∵AP⊥BP.PA⊥PC.∴AP⊥PBC 连PD.则PD就是AD在平面PBC上的射影 ∴∠PDA就是AD与平面PBC所成角 又∵∠ABP=∠ACP=60º.PB=PC=BC.D是BC中点. ∴PD=, PA=BC ∴AD= ∴ ∴AD与平面PBC所成角的余弦值为
网址:http://m.1010jiajiao.com/timu_id_3965957[举报]
如图,已知圆![]() 与
与![]() 轴负半轴的交点为
轴负半轴的交点为![]() . 由点
. 由点![]() 出发的射线
出发的射线![]() 的斜率为
的斜率为![]() . 射线
. 射线![]() 与圆
与圆![]() 相交于另一点
相交于另一点![]()

(1)当![]() 时,试用
时,试用![]() 表示点
表示点![]() 的坐标;
的坐标;
(2)当![]() 时,求证:“射线
时,求证:“射线![]() 的斜率
的斜率![]() 为有理数”是“点
为有理数”是“点![]() 为单位圆
为单位圆![]() 上的有理点”的充要条件;(说明:坐标平面上,横、纵坐标都为有理数的点为有理点.我们知道,一个有理数可以表示为
上的有理点”的充要条件;(说明:坐标平面上,横、纵坐标都为有理数的点为有理点.我们知道,一个有理数可以表示为![]() ,其中
,其中![]() 、
、![]() 均为整数且
均为整数且![]() 、
、![]() 互质)
互质)
(3)定义:实半轴长![]() 、虚半轴长
、虚半轴长![]() 和半焦距
和半焦距![]() 都是正整数的双曲线为“整勾股双曲线”.
都是正整数的双曲线为“整勾股双曲线”.
当![]() 为有理数且
为有理数且![]() 时,试证明:一定能构造偶数个“整勾股双曲线”(规定:实轴长和虚轴长都对应相等的双曲线为同一个双曲线),它的实半轴长、虚半轴长和半焦距的长恰可由点
时,试证明:一定能构造偶数个“整勾股双曲线”(规定:实轴长和虚轴长都对应相等的双曲线为同一个双曲线),它的实半轴长、虚半轴长和半焦距的长恰可由点![]() 的横坐标、纵坐标和半径
的横坐标、纵坐标和半径![]() 的数值构成. 说明你的理由并请尝试给出构造方法.
的数值构成. 说明你的理由并请尝试给出构造方法.
(本小题满分13分)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第![]() 层第
层第![]() 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为![]() .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
(Ⅰ)求![]() 的值,并猜想
的值,并猜想![]() 的表达式.(不必证明)
的表达式.(不必证明)
 (Ⅱ)设小弹子落入第6层第
(Ⅱ)设小弹子落入第6层第![]() 个竖直通道得到分数为
个竖直通道得到分数为![]() ,
,
其中![]() ,试求
,试求![]() 的分布列及数学期望.
的分布列及数学期望.

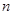 层第
层第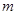 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为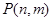 .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)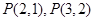 的值,并猜想
的值,并猜想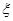 ,其中
,其中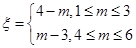 ,试求
,试求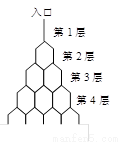
 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第