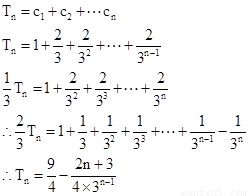摘要:2.等比数列的前n项和公式: 当时. ① 或 ② 当q=1时.
网址:http://m.1010jiajiao.com/timu_id_3965923[举报]
已知数列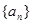 的前n项和
的前n项和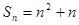 ,数列
,数列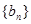 有
有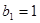 ,
,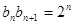
(1)求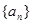 的通项;
的通项;
(2)若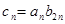 ,求数列
,求数列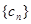 的前n项和
的前n项和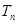 .
.
【解析】第一问中,利用当n=1时,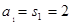
当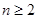 时,
时,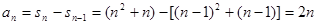
得到通项公式
第二问中,∵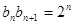 ∴
∴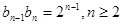 ∴数列
∴数列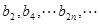 是以2为首项,2为公比的等比数列,利用错位相减法得到。
是以2为首项,2为公比的等比数列,利用错位相减法得到。
解:(1)当n=1时,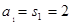 ……………………1分
……………………1分
当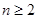 时,
时,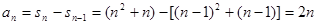 ……4分
……4分
又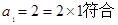
∴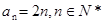 ……………………5分
……………………5分
(2)∵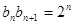 ∴
∴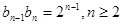
∴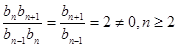 ……………………7分
……………………7分
又∵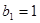 ,
,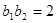 ∴
∴ 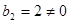
∴数列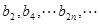 是以2为首项,2为公比的等比数列,
是以2为首项,2为公比的等比数列,
∴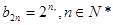 ……………………9分
……………………9分
∴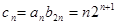
∴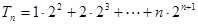 ①
①
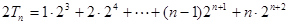 ②
②
①-②得: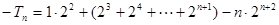
∴
查看习题详情和答案>>
设等比数列{an}的首项为a,公比q>0且q≠1,前n项和为Sn.
(Ⅰ)当a=1时,S1+1,S2+2,S3+1三数成等差数列,求数列{an}的通项公式;
(Ⅱ)对任意正整数n,命题甲:Sn,(Sn+1+1),Sn+2三数构成等差数列. 命题乙:Sn+1,(Sn+2+1),Sn+3三数构成等差数列.求证:对于同一个正整数n,命题甲与命题乙不能同时为真命题.
查看习题详情和答案>>
(Ⅰ)当a=1时,S1+1,S2+2,S3+1三数成等差数列,求数列{an}的通项公式;
(Ⅱ)对任意正整数n,命题甲:Sn,(Sn+1+1),Sn+2三数构成等差数列. 命题乙:Sn+1,(Sn+2+1),Sn+3三数构成等差数列.求证:对于同一个正整数n,命题甲与命题乙不能同时为真命题.
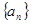 的前
的前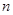 项的和为
项的和为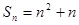 ,
,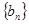 是等比数列,且
是等比数列,且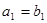 ,
,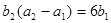 。
。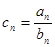 ,求数列
,求数列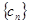 的前
的前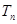 。
。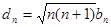 ,数列
,数列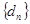 的前
的前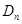 ,求证:
,求证: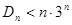 .
.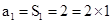 ;
;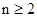 时,
时,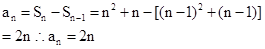
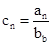 得:
得: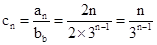 ,然后借助于错位相减法
,然后借助于错位相减法