题目内容
已知数列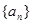 的前n项和
的前n项和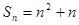 ,数列
,数列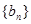 有
有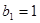 ,
,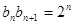
(1)求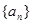 的通项;
的通项;
(2)若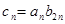 ,求数列
,求数列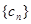 的前n项和
的前n项和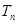 .
.
【解析】第一问中,利用当n=1时,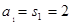
当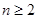 时,
时,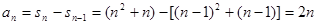
得到通项公式
第二问中,∵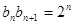 ∴
∴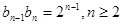 ∴数列
∴数列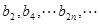 是以2为首项,2为公比的等比数列,利用错位相减法得到。
是以2为首项,2为公比的等比数列,利用错位相减法得到。
解:(1)当n=1时,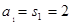 ……………………1分
……………………1分
当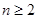 时,
时,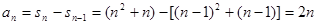 ……4分
……4分
又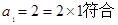
∴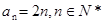 ……………………5分
……………………5分
(2)∵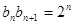 ∴
∴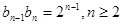
∴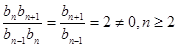 ……………………7分
……………………7分
又∵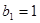 ,
,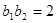 ∴
∴ 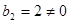
∴数列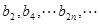 是以2为首项,2为公比的等比数列,
是以2为首项,2为公比的等比数列,
∴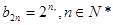 ……………………9分
……………………9分
∴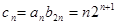
∴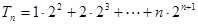 ①
①
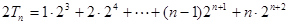 ②
②
①-②得: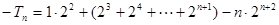
∴
【答案】
(1) (2)
(2)

练习册系列答案
相关题目
 的前n项和为
的前n项和为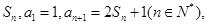 等差数列
等差数列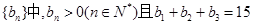 ,又
,又 成等比数列.
成等比数列. 的通项公式;
的通项公式; 的前n项和
的前n项和 .
. 的前n项和为
的前n项和为
 的通项公式;
的通项公式; ,求数列
,求数列 的前n项和
的前n项和 ;
; 对一切正整数n恒成立,求实数m的取值范围。
对一切正整数n恒成立,求实数m的取值范围。