摘要:12.(文)如图.△ABC中.在AC上取一点N.使得AN=AC. 在AB上取一点M.使得AM=AB.在BN的延长线上取 点P.使得NP=BN.在CM的延长线上取点Q.使得=λ时.=.试确定λ的值. 解:∵=-=(-) =(+)=. =-=+λ. 又∵=.∴+λ=. 即λ=.∴λ=. (理)如图.△ABC中.D为BC的中点.G为AD 的中点.过点G任作一直线MN分别交AB.AC于 M.N两点.若=x.=y.求+的值. 解:设=a.=b.则=xa.=yb. ==(+)=(a+b). ∴=-=(a+b)-xa=(-x)a+b. =-=yb-xa=-xa+yb. ∵与共线.∴存在实数λ.使=λ. ∴(-x)a+b=λ(-xa+yb)=-λxa+λyb. ∵a与b不共线.∴ 消去λ.得+=4.∴+为定值.
网址:http://m.1010jiajiao.com/timu_id_3965572[举报]
(08年聊城市四模文)(12分)如图是某几何体的直观图与三视图的侧视图、俯视图. 在直观图中,2BN=AE,M是ND的中点. 侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(1)在答题纸上的虚线框内画出该几何体的正视图,并标上数据;
(2)求证:EM∥平面ABC;
(3)求证:平面NDE⊥平面CEM.

(2009湖北卷文)如图,在三棱柱ABC-A1B1C1中,∠ACB=900,∠ACC1=600,∠BCC1=450,侧棱CC1的长为1,则该三棱柱的高等于
A.![]() B.
B.![]()
C.![]()
![]() D.
D.![]()

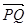 与
与 的夹角θ取何值时,
的夹角θ取何值时, 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。