摘要:一个袋中装有若干个大小相同的黑球.白球和红球.已知从袋中任意摸出1个球.得到黑球的概率是,从袋中任意摸出2个球.至少得到1个白球的概率是.若袋中共有10个球, (1)求白球的个数, (2)从袋中任意摸出3个球.记得到白球的个数为.求随机变量的数学期望E(). 解 (1)记“从袋中任意摸出两个球.至少得到一个白球 为事件A.设袋中白球的个数为x.则P(A)=1-. 得到x=5,故白球有5个. (2)随机变量的取值为0.1.2.3.概率分布是 0 1 2 3 P 的数学期望 E()= ×0+×1+×2+×3=.
网址:http://m.1010jiajiao.com/timu_id_3965103[举报]
一个袋中装有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是![]() ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是![]() .若袋中共有10个球,
.若袋中共有10个球,
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为![]() ,求随机变量
,求随机变量![]() 的数学期望E(
的数学期望E(![]() ).
).
一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.
(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于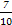 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.
一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.
(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于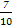 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.
 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于
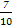 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.

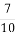
 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 ,
, .并指出袋中哪种颜色的球个数最少.
.并指出袋中哪种颜色的球个数最少.