摘要：是函数在点xo处存在极限的( ) 必要不充分条件 既不充分也不必要条件
网址：http://m.1010jiajiao.com/timu_id_3963958[举报]
（2012•宿州三模）设函数f（x）=p（x-
）-2lnx，g（x）=
．（p是实数，e是自然对数的底数）
（1）当p=2时，求与函数y=f（x）的图象在点A（1，0）处相切的切线方程；
（2）若f（x）在其定义域内为单调递增函数，求p的取值范围；
（3）若在[1，e]上至少存在一点xo，使得f（x0）＞g（x0）成立，求p的取值范围．
查看习题详情和答案>>
| 1 |
| x |
| 2e |
| x |
（1）当p=2时，求与函数y=f（x）的图象在点A（1，0）处相切的切线方程；
（2）若f（x）在其定义域内为单调递增函数，求p的取值范围；
（3）若在[1，e]上至少存在一点xo，使得f（x0）＞g（x0）成立，求p的取值范围．
设函数f（x）=p（x-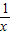
）-2lnx，g（x）=
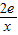．（p是实数，e是自然对数的底数）
（1）当p=2时，求与函数y=f（x）的图象在点A（1，0）处相切的切线方程；
（2）若f（x）在其定义域内为单调递增函数，求p的取值范围；
（3）若在[1，e]上至少存在一点xo，使得f（x）＞g（x）成立，求p的取值范围．
查看习题详情和答案>>
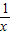）-2lnx，g（x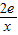）=．（p是实数，e是自然对数的底数）（1）当p=2时，求与函数y=f（x）的图象在点A（1，0）处相切的切线方程；
（2）若f（x）在其定义域内为单调递增函数，求p的取值范围；
（3）若在[1，e]上至少存在一点xo，使得f（x）＞g（x）成立，求p的取值范围．
查看习题详情和答案>>
设函数f（x）=p（x-
）-2lnx，g（x）=
．（p是实数，e是自然对数的底数）
（1）当p=2时，求与函数y=f（x）的图象在点A（1，0）处相切的切线方程；
（2）若f（x）在其定义域内为单调递增函数，求p的取值范围；
（3）若在[1，e]上至少存在一点xo，使得f（x）＞g（x）成立，求p的取值范围．
查看习题详情和答案>>
）-2lnx，g（x）=．（p是实数，e是自然对数的底数）（1）当p=2时，求与函数y=f（x）的图象在点A（1，0）处相切的切线方程；
（2）若f（x）在其定义域内为单调递增函数，求p的取值范围；
（3）若在[1，e]上至少存在一点xo，使得f（x）＞g（x）成立，求p的取值范围．
查看习题详情和答案>>
）-2lnx，g（x）=
．（p是实数，e是自然对数的底数）