频率分布:用样本估计总体.是研究统计问题的基本思想方法.样本中所有数据的频数和样本容量的比.就是该数据的频率.所有数据的频率的分布变化规律叫做样本的频率分布.可以用样本频率表.样本频率分布条形图或频率——青夏教育精英家教网——

摘要：频率分布:用样本估计总体.是研究统计问题的基本思想方法.样本中所有数据的频数和样本容量的比.就是该数据的频率.所有数据的频率的分布变化规律叫做样本的频率分布.可以用样本频率表.样本频率分布条形图或频率分布直方图来表示.

网址：http://m.1010jiajiao.com/timu_id_3963747[举报]

某校300名学生，会考化学得分范围是70-119（得分都是整数），为了了解该校这300名学生的会考化学成绩，从中抽查了一部分学生的化学分数，通过数据处理，得到如下频率分布表和频率分布直方图．

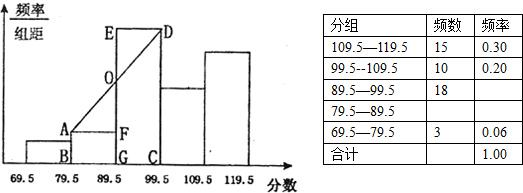
请你根据给出的图标解答：
（1）填写频率分布表中未完成部分的数据；
（2）指出在这个问题中的总体和样本容量；
（3）求出在频率分布直方图中直角梯形ABCD的面积；
（4）请你用样本估计总体，可以得到哪些信息？（写一条即可）查看习题详情和答案>>

青少年的视力水平的下降已经引起全社会的关注，某校为了了解高二年级500名学生的视力情况，从中抽查一部分学生视力，通过数据处理，得到如下频率分布表．可是粗心的调查员却把表中的五个数据抄丢了．

分组	频数	频率
3.95～4.25	2	0.04
4.25～4.55	n₁	0.12
4.55～4.85	25	m₁
4.85～5.15	n₂	m₂
5.15～5.45	2	0.04
合计	N	1.00

（1）聪明的你能够帮助调查员找回丢失的数据吗？
（2）请你帮助调查员在给出的坐标系中画出频率分布直方图，请你标出横、纵轴代表的量；（数据保留两位小数）
（3）用样本估计总体，可以得到哪些信息？（写一条即可）．

查看习题详情和答案>>

某学校高三年级有学生1000名，经调查研究，其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼（称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学．
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表

	身高达标	身高不达标	总计
积极参加体育锻炼	40
不积极参加体育锻炼		15
总计			100

（ⅰ）完成上表；
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K²=

(a+b)(c+d)(a+c)(b+d)

，参考数据：

P（K²≥k）	0.40	0.25	0.15	0.10	0.05	0.025
k	0.708	1.323	2.072	2.706	3.841	5.024

查看习题详情和答案>>

为调查某市学生百米运动成绩，从该市学生中按照男女生比例随机抽取50名学生进行百米测试，学生成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图，根据有关规定，成绩小于16秒为达标．
（Ⅰ）用样本估计总体，某班有学生45人，设ξ为达标人数，求ξ的数学期望与方差；
（Ⅱ）如果男女生使用相同的达标标准，则男女生达标情况如表：

性别是否达标	男	女	合计
达标	a=24	b= 6 6	30 30
不达标	c= 8 8	d=12	20 20
合计	32 32	18 18

根据表中所给的数据，能否有99%的把握认为“体育达标与性别有关”？若有，你能否提出一个更好的解决方法来？
附：

P（K²≥K）	0.050	0.010	0.001
K	3.841	6.625	10.828

(a+b)(c+d)(a+c)(b+d)

查看习题详情和答案>>

从某节能灯生产线上随机抽取100件产品进行寿命试验，按连续使用时间（单位：天）共分5组，得到频率分布直方图如图．
（I）以分组的中点数据作为平均数据，用样本估计该生产线所生产的节能灯的预期连续使用寿命；
（II）为了分析使用寿命差异较大的产品，从使用寿命低于200天和高于350天的产品中用分层抽样的方法共抽取6件，求样品A被抽到的概率．

查看习题详情和答案>>