摘要：已知函数满足且在R上恒成立. 求的值. 是否存在实数m,使函数在区间上有最小值-5?若存在.请求出实数m的值,若不存在.请说明理由. 附加题: 已知函数在x=1处取得极值2. 的解析式, 上除原点O外的任意一点.过OA的中点且垂直于x轴的直线交曲线于点B.试问:是否存在这样的点A.使得曲线在点B处的切线与OA平行?若存在.求出点A的坐标,若不存在.说明理由. (3) 设函数.若对于任意的.总存在.使得.求实数a的取值范围.
网址：http://m.1010jiajiao.com/timu_id_3961340[举报]
已知函数
满足：对于任意实数
，都有
恒成立，且当
时，
恒成立；
(1)求
的值，并例举满足题设条件的一个特殊的具体函数；
(2)判定函数
在R上的单调性，并加以证明；
(3)若函数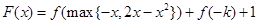
(其中
)有三个零点
,求
的取值范围.
查看习题详情和答案>>
已知函数f（x）=ax2+bx+c满足：f（1）=3，且f（x）在R上为奇函数．
（1）求函数f（x）的解析式；
（2）设Sn=f(
)+f(
)+f(
)+…+f(
)，若不等式
＜
对n∈N+恒成立，求实数m的取值范围；
（3）若数列{an}，{bn}满足：a1=1，an+1=
；b1=1，bn+1-bn=
，记g(n)=
，问是否存在k∈N，使g（k+1）=2g（k）成立，若存在，求出k值；若不存在，说明理由．
查看习题详情和答案>>
（1）求函数f（x）的解析式；
（2）设Sn=f(
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n |
| n |
| mn |
| Sn |
| mn+1 |
| Sn+1 |
（3）若数列{an}，{bn}满足：a1=1，an+1=
| f(an) |
| 2f(an)+3 |
| 1 |
| an |
|
已知函数f（x）（x∈R）满足：对于任意实数x，y，都有f(x+y)=f(x)+f(y)+
恒成立，且当x＞0时，f(x)＞-
恒成立；
（1）求f（0）的值，并例举满足题设条件的一个特殊的具体函数；
（2）判定函数f（x）在R上的单调性，并加以证明；
（3）若函数F（x）=f（max{-x，2x-x2}）+f（-k）+1（其中max{a，b}=
）有三个零点x1，x2，x3，求u=（x1+x2+x3）+x1•x2•x3的取值范围．
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
（1）求f（0）的值，并例举满足题设条件的一个特殊的具体函数；
（2）判定函数f（x）在R上的单调性，并加以证明；
（3）若函数F（x）=f（max{-x，2x-x2}）+f（-k）+1（其中max{a，b}=
|
已知函数f（x）=ax2+4ax+b-1（a≠0且a，b∈R），不等式|f（x）|≤|2x2+8x-10|恒成立．
（Ⅰ）求证：-5和1是函数f（x）的两个零点；并求实数a，b满足的关系式；
（Ⅱ）求函数f（x）在区间[a，2]（a＜2）上的最小值g（a）；
（Ⅲ）令F（x）=
，若mn＜0，m+n＞0，试确定F（m）+F（n）的符号，并说明理由．
查看习题详情和答案>>
（Ⅰ）求证：-5和1是函数f（x）的两个零点；并求实数a，b满足的关系式；
（Ⅱ）求函数f（x）在区间[a，2]（a＜2）上的最小值g（a）；
（Ⅲ）令F（x）=
|
已知函数f（x）=ax+bsinx，当x=
时，f（x）取得极小值
-
．
（1）求a，b的值；
（2）设直线l：y=g（x），曲线S：y=F（x）．若直线l与曲线S同时满足下列两个条件：
①直线l与曲线S相切且至少有两个切点；
②对任意x∈R都有g（x）≥F（x）．则称直线l为曲线S的“上夹线”．
试证明：直线l：y=x+2是曲线S：y=ax+bsinx的“上夹线”．
（3）记h(x)=
[5x-f(x)]，设x1是方程h（x）-x=0的实数根，若对于h（x）定义域中任意的x2、x3，当|x2-x1|＜1，且|x3-x1|＜1时，问是否存在一个最小的正整数M，使得|h（x3）-h（x2）|≤M恒成立，若存在请求出M的值；若不存在请说明理由．
查看习题详情和答案>>
| π |
| 3 |
| π |
| 3 |
| 3 |
（1）求a，b的值；
（2）设直线l：y=g（x），曲线S：y=F（x）．若直线l与曲线S同时满足下列两个条件：
①直线l与曲线S相切且至少有两个切点；
②对任意x∈R都有g（x）≥F（x）．则称直线l为曲线S的“上夹线”．
试证明：直线l：y=x+2是曲线S：y=ax+bsinx的“上夹线”．
（3）记h(x)=
| 1 |
| 8 |