摘要：例1 求证:如果两条直线同垂直于一个平面.则这两条直线平行 已知:直线于.于． 求证:． 证明:以为原点.射线为非负轴.建立空间直角坐标系. 分别为沿轴.轴.轴的坐标向量. 设. ∵.∴.. . . ∴.即. 又知.为两个不同的点.∴． 点评:如果表示向量的有向线段所在直线垂直于平面.记作.此时向量叫做平面的法向量． 例2．在棱长为的正方体中.分别是中点.在棱上..是的中点. (1)求证:, (2)求与所成的角的余弦, (3)求的长 解:如图以为原点建立直角坐标系. 则.... ... (1).. ∴. ∴． (2)∵. ∴. .. ∴. ∴与所成的角的余弦． (3)∵. ∴． 例3．已知点是平行四边形所在平面外一点.如果.. (1)求证:是平面的法向量, (2)求平行四边形的面积． (1)证明:∵. . ∴..又.平面. ∴是平面的法向量． (2).. ∴. ∴. ∴. ∴． 例4 在长方体ABCD-A1B1C1D1中.AB＝a.BC＝b.AA1＝c.求异面直线BD1和B1C所成角的余弦值 分析一:利用.以及数量积的定义.可求出cos＜＞.从而得到异面直线BD1和B1C所成角的余弦值 分析二:建立空间直角坐标系.利用向量.且将向量的 运算转化为实数的运算.以达到证明的目的 解:建立如图所示空间直角坐标系.使D为坐标原点. 则B,D1,B1 设异面直线BD1和B1C所成角为θ.则
网址：http://m.1010jiajiao.com/timu_id_3959973[举报]
设椭圆C：
（a＞b＞0）的一个顶点坐标为A（
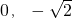），且其右焦点到直线
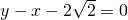的距离为3．
（1）求椭圆C的轨迹方程；
（2）若A、B是椭圆C上的不同两点，弦AB（不平行于y轴）的垂直平分线与x轴相交于点M，则称弦AB是点M的一条“相关弦”，如果点M的坐标为M（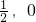
），求证：点M的所有“相关弦”的中点在同一条直线上；
（3）对于问题（2），如果点M坐标为M（t，0），当t满足什么条件时，点M（t，0）存在无穷多条“相关弦”，并判断点M的所有“相关弦”的中点是否在同一条直线上．
查看习题详情和答案>>
设椭圆C：（a＞b＞0）的一个顶点坐标为A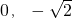（），且其右焦点到直线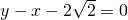的距离为3．
（1）求椭圆C的轨迹方程；
（2）若A、B是椭圆C上的不同两点，弦AB（不平行于y轴）的垂直平分线与x轴相交于点M，则称弦AB是点M的一条“相关弦”，如果点M的坐标为M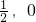（），求证点M的所有“相关弦”的中点在同一条直线上；
（3）根据解决问题（2）的经验与体会，请运用类比、推广等思想方法，提出一个与“相关弦”有关的具有研究价值的结论，并加以解决．（本小题将根据所提出问题的层次性给予不同的分值）
查看习题详情和答案>>
设椭圆C：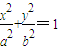
（a＞b＞0）的一个顶点坐标为A（
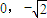），且其右焦点到直线
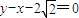的距离为3．
（1）求椭圆C的轨迹方程；
（2）若A、B是椭圆C上的不同两点，弦AB（不平行于y轴）的垂直平分线与x轴相交于点M，则称弦AB是点M的一条“相关弦”，如果点M的坐标为M（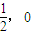
），求证：点M的所有“相关弦”的中点在同一条直线上；
（3）对于问题（2），如果点M坐标为M（t，0），当t满足什么条件时，点M（t，0）存在无穷多条“相关弦”，并判断点M的所有“相关弦”的中点是否在同一条直线上．
查看习题详情和答案>>
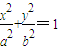（a＞b＞0）的一个顶点坐标为A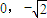（），且其右焦点到直线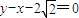的距离为3．（1）求椭圆C的轨迹方程；
（2）若A、B是椭圆C上的不同两点，弦AB（不平行于y轴）的垂直平分线与x轴相交于点M，则称弦AB是点M的一条“相关弦”，如果点M的坐标为M（
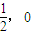），求证：点M的所有“相关弦”的中点在同一条直线上；（3）对于问题（2），如果点M坐标为M（t，0），当t满足什么条件时，点M（t，0）存在无穷多条“相关弦”，并判断点M的所有“相关弦”的中点是否在同一条直线上．
查看习题详情和答案>>
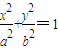（a＞b＞0）的一个顶点坐标为A（
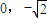），且其右焦点到直线
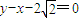的距离为3．
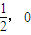），求证点M的所有“相关弦”的中点在同一条直线上；