摘要:18.设数列{an}满足a1=t.a2=t2.前n项和为Sn.且Sn+2-(t+1)Sn+1+tSn=0(n∈N*). (1)证明数列{an}为等比数列.并求{an}的通项公式, (2)当<t<2时.比较2n+2-n与tn+t-n的大小, (3)若<t<2.bn=.求证:++-+<2n-2-. 解:(1)证明:由Sn+2-(t+1)Sn+1+tSn=0.得tSn+1-tSn=Sn+2-Sn+1.即an+2=tan+1. 而a1=t.a2=t2.∴数列{an}是以t为首项.t为公比的等比数列. ∴an=tn. (2)∵(tn+t-n)-(2n+2-n)=(tn-2n)[1-()n].又<t<2.∴<<1.则tn-2n<0且1-()n>0. ∴(tn-2n)[1-()n]<0.∴tn+t-n<2n+2-n. (3)证明:∵=(tn+t-n). ∴2<(2+22+-2n)+(2-1+2-2+-+2-n)=2(2n-1)+1-2-n=2n+1-(1+2-n)<2n+1-2. ∴++-+<2n-2-.
网址:http://m.1010jiajiao.com/timu_id_3959835[举报]
(本小题满分12分)
已知数列{an}满足a1=0,a2=2,且对任意m、n∈N*都有
a2m-1+a2n-1=2am+n-1+2(m-n)2
(Ⅰ)求a3,a5;
(Ⅱ)设bn=a2n+1-a2n-1(n∈N*),证明:{bn}是等差数列;
(Ⅲ)设cn=(an+1-an)qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
查看习题详情和答案>> .
. ,记数列{bn}的前n项为Tn,求Tn.
,记数列{bn}的前n项为Tn,求Tn.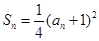 .
.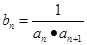 ,记数列{bn}的前n项为Tn,求Tn.
,记数列{bn}的前n项为Tn,求Tn.