摘要：16．如图是函数f(x)＝Asin(ωx+φ)(A＞0.ω＞0.-π＜φ＜π).x∈R的部分图象.则下列命题中.正确命题的序号为 ． ①函数f(x)的最小正周期为, ②函数f(x)的振幅为2, ③函数f(x)的一条对称轴方程为x＝, ④函数f(x)的单调递增区间为[.], ⑤函数的解析式为f(x)＝sin(2x-)． 解析:由图象可知.函数f(x)的最小正周期为(-)×2＝π.故①不正确,函数f(x)的振幅为.故②不正确,函数f(x)的一条对称轴方程为x＝＝.故③正确,④不全面.函数f(x)的单调递增区间应为[+2kπ.+2kπ].k∈Z,由sin(2×+φ)＝得2×+φ＝+2kπ.k∈Z.即φ＝2kπ-.k∈Z.∵-π＜φ＜π.故k取0.从而φ＝-.故f(x)＝sin(2x-)． 答案:③⑤
网址：http://m.1010jiajiao.com/timu_id_3959089[举报]
函数f(x)＝Asin(ωx＋φ)（A＞0，ω＞0）的部分图象如图所示，下列结论：
①将f(x)的图像向左平移
个单位，所得到的函数是偶函数；
②f(x)的最小正周期为p； ③f(0)＝1；
④f(
)＜f(
)； ⑤f(x)＝－f(
－x)．
其中正确的是
（A）①②③ （B）②③④
（C）①④⑤ （D）②④⑤
查看习题详情和答案>>函数f(x)＝Asin(wx＋
)，(A)＞0，w＞0，||＜
)的一系列对应值如下表：
(1)根据表中数据求出f(x)的解析式；
(2)指出函数f(x)的图象是由函数y＝sinx(x∈R)的图象经过怎样的变化而得到的；
(3)令g(x)＝f(x＋
)－a，若g(x)在x∈[－
，
]时有两个零点，求a的取值范围．
已知函数f(x)＝asinωx＋bcosωx部分图像，如图所示(a，b，ω∈R，且ω＞0)．
(1)求a，b，ω的值；
(2)设关于t的方程t2＋mt＋n＝0(m，n∈R，且m≠0)有两个不等实数根；
①若|m|＋|n|＜1，证明f2(x)＋mf(x)＋n＝0在(－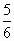
π，
)内有两个不等实数根；
②上述①的逆命题是否成立，并给出证明．
)的图象(部分)如图所示，则f(x)的解析式是
x＋
x＋
)的图象(部分)如图所示，则f(x)的解析式是
x＋
x＋