题目内容
已知函数f(x)＝asinωx＋bcosωx部分图像，如图所示(a，b，ω∈R，且ω＞0)．
(1)求a，b，ω的值；
(2)设关于t的方程t2＋mt＋n＝0(m，n∈R，且m≠0)有两个不等实数根；
①若|m|＋|n|＜1，证明f2(x)＋mf(x)＋n＝0在(－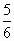
π，
)内有两个不等实数根；
②上述①的逆命题是否成立，并给出证明．
答案：
解析：
解析：
|
解 (1)由图像易知函数f(x)的周期为T＝4 ∴ω＝1．上述函数的图像是由y＝sinx的图像沿x轴负方向平移 ∴a＝ (2)①由|m|＋|n|≤1得|m＋n|≤|m|＋|n|＜1，∴m＋n＞－1． 同样|m－n|≤|m|＋|n|＜1，∴m－n＜1． 令g(t)＝t2＋mt＋n，显然g(1)＝m＋n＋1＞0，g(－1)＝1－m＋n＞0． 而二次函数g(t)的对称轴t＝－ ∴二次方程t2＋mt＋n＝0两实根在(－1，1)中． ∴关于x的方程在sin2(x＋ ②逆命题不成立． 反例，关于t的方程为t2＋ 显然方程sin2(x＋ |
＝2π，
个单位得到的，其解析式为f(x)＝sin(x＋
，b＝
．
∈(－1，1)，
)内有两个不同实根．
t＋
＝0，
＝1．
练习册系列答案
教学练新同步练习系列答案
相关题目
(a、b为常数)，且方程f(x)－x＋12＝0有两个实根为x1＝3，x2＝4.
.
(a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
)