摘要:12.在△ABC中.内角A.B.C的对边分别为a.b.c.<C<且= (1)判断△ABC的性状, (2)若|+|=2.求·的取值范围. 解:(1)由=及正弦定理得sinB=sin2C. ∴B=2C.且B+2C=π. 若B=2C.<C<. ∴π<B<π.B+C>π(舍), ∴B+2C=π.则A=C.∴△ABC为等腰三角形. (2)∵|+|=2.∴a2+c2+2ac·cosB=4. ∴cosB=(∵a=c). 而cosB=-cos2C.<C<. ∴<cosB<1. ∴1<a2<. 又·=accosB=2-a2.∴·∈(.1). 在△ABC中.A.B.C分别是三边a.b.c的对角.设m=.n=.m.n的夹角为. (1)求C的大小, (2)已知c=.三角形的面积S=.求a+b的值. 解:(1)m·n=cos2-sin2=cosC. 又m·n=|m||n|cos=. 故cosC=.∵0<C<π.∴C=. (2)S=absinC=absin=ab. 又已知S=.故ab=.∴ab=6. ∵c2=a2+b2-2abcosC.c=. ∴=a2+b2-2ab×=(a+b)2-3ab. ∴(a+b)2=+3ab=+18=. ∴a+b=.
网址:http://m.1010jiajiao.com/timu_id_3959061[举报]
(2010•珠海二模)(文)在△ABC中,A点的坐标为(3,0),BC边长为2,且BC在y轴上的区间[-3,3]上滑动.
(1)求△ABC外心的轨迹方程;
(2)设直线l:y=3x+b与(1)的轨迹交于E,F两点,原点到直线l的距离为d,求
的最大值.并求出此时b的值.
查看习题详情和答案>>
(1)求△ABC外心的轨迹方程;
(2)设直线l:y=3x+b与(1)的轨迹交于E,F两点,原点到直线l的距离为d,求
| |EF| | d |
 (2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理)设{an}的公差d(d>0)为已知常数,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?并请说明理由.
(4)(文)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.
(2010湖北文数)10.记实数![]() …
…![]() 中的最大数为
中的最大数为![]() {
{![]() …
…![]() },最小数为min{
},最小数为min{![]() …
…![]() }.已知
}.已知![]() 的三边边长为
的三边边长为![]() 、
、![]() 、
、![]() (
(![]() ),定义它的倾斜度为
),定义它的倾斜度为
![]()
则“t=1”是“![]() 为等边三解形”的
为等边三解形”的
A,充分布不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分也不必要的条件
查看习题详情和答案>>(2010湖北文数)10.记实数![]() …
…![]() 中的最大数为
中的最大数为![]() {
{![]() …
…![]() },最小数为min{
},最小数为min{![]() …
…![]() }.已知
}.已知![]() 的三边边长为
的三边边长为![]() 、
、![]() 、
、![]() (
(![]() ),定义它的倾斜度为
),定义它的倾斜度为
![]()
则“t=1”是“![]() 为等边三解形”的
为等边三解形”的
A,充分布不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分也不必要的条件
查看习题详情和答案>>
已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数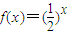 的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理)设{an}的公差d(d>0)为已知常数,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?并请说明理由.
(4)(文)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.
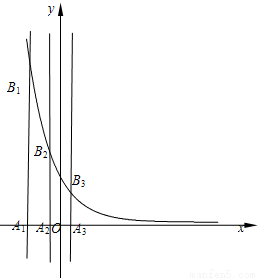 查看习题详情和答案>>
查看习题详情和答案>>
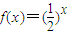 的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理)设{an}的公差d(d>0)为已知常数,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?并请说明理由.
(4)(文)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>