摘要：19．在图23-A-10中.把△ABC向右平移5个方格.再绕点B的对应点顺时针方向旋转90度． (1)画出平移和旋转后的图形.并标明对 应字母, (2)能否把两次变换合成一种变换.如 果能.说出变换过程,如果不能.说明理由．
网址：http://m.1010jiajiao.com/timu_id_3957661[举报]
（2012•北京）近年来，北京市大力发展轨道交通，轨道运营里程大幅增加，2011年北京市又调整修订了2010至2020年轨道交通线网的发展规划．以下是根据北京市轨道交通指挥中心发布的有关数据制作的统计图表的一部分．北京市轨道交通已开通线路相关数据统计表（截止2010年底）
| 开通时间 | 开通线路 | 运营里程（千米） |
| 1971 | 1号线 | 31 |
| 1984 | 2号线 | 23 |
| 2003 |
13号线 | 41 |
| 八通线 | 19 | |
| 2007 | 5号线 | 28 |
| 2008 |
8号线 | 5 |
| 10号线 | 25 | |
| 机场线 | 28 | |
| 2009 | 4号线 | 28 |
2010 |
房山线 | 22 |
| 大兴线 | 22 | |
| 亦庄线 | 23 | |
| 昌平线 | 21 | |
| 15号线 | 20 |
（1）补全条形统计图并在图中标明相应数据；
（2）按照2011年规划方案，预计2020年北京市轨道交通运营总里程将达到多少千米？
（3）要按时完成截至2015年的轨道交通规划任务，从2011到2015年这4年中，平均每年需新增运营里程多少千米？
第29届奥运会在我国胜利的召开，我们参赛的运动员所表现出的顽强意志和获得的优异成绩跟我们留下了深深的回忆，特别是10米女子跳水冠军郭晶晶的优美姿势深深地打动了我们．下面是一位外国跳水运动员在进行某次10米跳台跳水训练时，测得身体（看成一点）在空中的运动路线是抛物线y=-| 25 |
| 6 |
| 2 |
| 5 |
| 2 |
| 3 |
（1）运动员在空中运动的最大高度离水面为多少米？
（2）如果运动员在距水面高度为5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误．在这次试跳中，运动员在空中调整好入水姿势时，测得距池边的水平距离为3
| 3 |
| 5 |
近五十年来，我国土地荒漠化扩展的面积及沙尘暴发生的次数情况如表1，表2所示．
表1：土地荒漠化扩展的面积情况
表2：沙尘暴发生的次数情况
（1）求出五十年来平均每年土地荒漠化扩展的面积；
（2）在图中画出不同年代沙尘暴发生的次数的折线图；
（3）观察表2或（2）所得的折线图，你认为沙尘暴发生次数呈 （选择“增加”，“稳定”或“减少”）趋势．
查看习题详情和答案>>
表1：土地荒漠化扩展的面积情况
| 年代 | 50，60年代的20年 | 70，80年代的20年 | 90年代的20年 |
| 平均每年土地荒漠化扩展的面积（km2） | 1560 | 2100 | 2460 |
| 年代 | 50年代的10年 | 60年代的10年 | 70年代的10年 | 80年代的10年 | 90年代的10年 |
| 每十年沙尘暴发生次数 | 5 | 8 | 13 | 14 | 23 |
（2）在图中画出不同年代沙尘暴发生的次数的折线图；
（3）观察表2或（2）所得的折线图，你认为沙尘暴发生次数呈
查看习题详情和答案>>
如图：四边形ABCD中，AD∥BC，∠B=∠C，AD=a（a＞0），BC=8，AD、BC间的距离为2
，有一边长为2的等边△EFG，在四边形ABCD内作任意运动，在运动过程中始终保持EF∥BC．记△EFG在四边形ABCD内部运动过程中“能够扫到的部分”的面积为S．
（1）如图①所示，当a=8时，△EFG在四边形ABCD内部运动过程中“能够扫到的部分”即为六边形HIBCJK，则S= ；
（2）如图②所示，当a=10时，求S的值；
（3）如图③所示，当a=2时，求S的值．
查看习题详情和答案>>
| 3 |
（1）如图①所示，当a=8时，△EFG在四边形ABCD内部运动过程中“能够扫到的部分”即为六边形HIBCJK，则S=
（2）如图②所示，当a=10时，求S的值；
（3）如图③所示，当a=2时，求S的值．
查看习题详情和答案>>
（1）解不等式：
-1＞
（2）做一做：
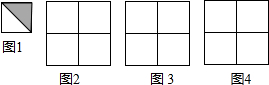
用四块如图1的瓷砖拼成一个正方形，使拼成的图案成轴对称图形，请你在图2，图3，图4中各画出一种拼法（要求三种拼法各不相同，所画图案中的阴影部分用斜线表示）
（3）读一读：
式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和．
由于上述式子比较长，书写也不方便，为了简便起见，我们可以将
“1+2+3+4+5+…+100”表示为
n，这里“Σ”是求和符号．
例如：“1+3+5+7+9+…+99”（即从1开始的100以内的连续奇数的和）可表示为
(2n-1)；又如：“13+23+33+43+53+63+73+83+93+103”可表示为
n3．
同学们，通过对以上材料的阅读，请解答下列问题：
＜1＞2+4+6+8+10+…+100（即从2开始的100以内的连续偶数的和）用求和符号可表示为 ；
＜2＞计算：
(n2-1)= （填写最后的计算结果）．
查看习题详情和答案>>
| x-3 |
| 2 |
| x-5 |
| 3 |
（2）做一做：
用四块如图1的瓷砖拼成一个正方形，使拼成的图案成轴对称图形，请你在图2，图3，图4中各画出一种拼法（要求三种拼法各不相同，所画图案中的阴影部分用斜线表示）
（3）读一读：
式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和．
由于上述式子比较长，书写也不方便，为了简便起见，我们可以将
“1+2+3+4+5+…+100”表示为
| 100 |
 |
| n=1 |
例如：“1+3+5+7+9+…+99”（即从1开始的100以内的连续奇数的和）可表示为
| 50 |
|
| n=1 |
| 10 |
|
| n=1 |
同学们，通过对以上材料的阅读，请解答下列问题：
＜1＞2+4+6+8+10+…+100（即从2开始的100以内的连续偶数的和）用求和符号可表示为
＜2＞计算：
| 5 |
|
| n=1 |