摘要：13．若a+b+c=0.且a≠0.则一元二次方程ax2+bx+c=0必有一个定根.它是 ．
网址：http://m.1010jiajiao.com/timu_id_3954840[举报]
对于一元二次方程ax2+bx+c=0（a≠0），下列说法：
①若
+
=-1，则方程ax2+bx+c=0一定有一根是x=1；
②若c=a3，b=2a2，则方程ax2+bx+c=0有两个相等的实数根；
③若a＜0，b＜0，c＞0，则方程cx2+bx+a=0必有实数根；
④若ab-bc=0，且
＜-1，则方程cx2+bx+a=0的两实数一定互为相反数．其中正确的结论是（ ）
①若
| a |
| c |
| b |
| c |
②若c=a3，b=2a2，则方程ax2+bx+c=0有两个相等的实数根；
③若a＜0，b＜0，c＞0，则方程cx2+bx+a=0必有实数根；
④若ab-bc=0，且
| a |
| c |
| A、①②③④ | B、①②④ |
| C、①③ | D、②④ |
已知一元二次方程ax2+bx+c=0（a≠0）．下列说法：①若a+b+c=0，则b2-4ac≥0；②若方程两根为-1和2，则2a+c=0；③若2a+b=0，且方程有一根大于2，则另一根必为负数；④若b=2a+3c，则方程有两个不相等的实根．其中正确的有（ ）
查看习题详情和答案>>
对于一元二次方程ax2+bx+c=O(a≠0)，下列说法：
①若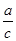
+
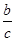=-1，则方程ax2+bx+c=O 一定有一根是x=1;
②若c=a3，b=2a2，则方程ax2+bx+c=O有两个相等的实数根；
③若a<0，b<0，c>0，则方程cx2+bx+a=0必有实数根；
④若ab-bc=0且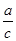<-l，则方程cx2+bx+a=0的两实数根一定互为相反数．．
其中正确的结论是( )
A．①②③④ B．①②④ C．①③ D．②④
查看习题详情和答案>>