摘要:22. 已知在区间上是增函数 (I)求实数的取值范围, (II)记实数的取值范围为集合A.且设关于的方程的两个非零实根为. ①求的最大值, ②试问:是否存在实数m.使得不等式对及恒成立?若存在.求m的取值范围,若不存在.请说明理由. , 2010届厦门双十中学高三数学-热身考试卷答题卡 (说明:大题的答案必须写在虚线内.否则无效,必须用黑色签字笔书写)
网址:http://m.1010jiajiao.com/timu_id_3953660[举报]
(本小题满分14分)
已知函数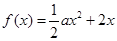 ,
,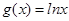 .
.
(1)如果函数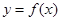 在
在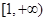 上是单调增函数,求
上是单调增函数,求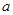 的取值范围;
的取值范围;
(2)是否存在实数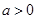 ,使得方程
,使得方程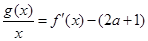 在区间
在区间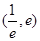 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出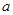 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
(本小题满分14分)
已知函数f(x)=(1+x)2-aln(1+x)2在(-2,-1)上是增函数,在(-∞,-2)上为减函数.
(1)求f(x)的表达式;
(2)若当x∈![]() 时,不等式f(x)<m恒成立,求实数m的值;
时,不等式f(x)<m恒成立,求实数m的值;
(3)是否存在实数b使得关于x的方程f(x)=x2+x+b在区间[0,2]上恰好有两个相异的实根,若存在,求实数b的取值范围.
查看习题详情和答案>>(本小题满分14分)
已知函数f(x)=(1+x)2-aln(1+x)2在(-2,-1)上是增函数,在(-∞,-2)上为减函数.
(1)求f(x)的表达式;
(2)若当x∈![]() 时,不等式f(x)<m恒成立,求实数m的值;
时,不等式f(x)<m恒成立,求实数m的值;
(3)是否存在实数b使得关于x的方程f(x)=x2+x+b在区间[0,2]上恰好有两个相异的实根,若存在,求实数b的取值范围.
查看习题详情和答案>>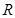 上的函数
上的函数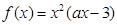 ,其中
,其中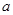 为常数。
为常数。 时,函数
时,函数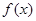 取得极值,求
取得极值,求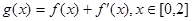 ,在
,在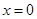 处取得最大值,求正数
处取得最大值,求正数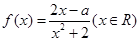
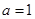 时,求曲线
时,求曲线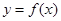 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间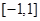 上是增函数,求实数
上是增函数,求实数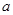 的取值范围
的取值范围 ;
;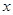 的方程
的方程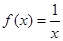 的两个根为
的两个根为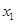 、
、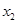 ,若对任意
,若对任意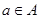 ,
,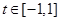 ,不等式
,不等式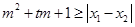 恒成立,求
恒成立,求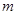 的取值范围.
的取值范围.