摘要：16 已知向量m=和n=(-sinθ,cosθ),θ∈［π,2π］. (1)求|m+n|的最大值, (2)当|m+n|=时,求cos()的值. 解:(1)m+n=(cosθ-sinθ+,cosθ+sinθ), |m+n|= = 2分 = =2 4分 ∵θ∈［π,2π］,∴,∴cos(θ+)≤1,|m+n|max=2. 6分 (2)由已知|m+n|=,得cos(θ+)=. 8分 又cos(θ+)=2cos2()-1,∴cos2()=, 10分 ∵θ∈［π,2π］,∴,∴cos(. 12分17． 已知命题:“函数在上存在零点 , 命题:“只有一个实数满足不等式 .若命题或是假命题.求实数的取值范围． 解:函数在上存在零点 ∴方程有解 显然或 --------------2分 ∵.故或 ∴ --------------4分 只有一个实数满足即抛物线与x轴只有一个交点 ∴ 或 --------------8分 ∴命题或为真命题时.或 ∵命题或为假命题 ∴的取值范围为--------------12分
网址：http://m.1010jiajiao.com/timu_id_3952830[举报]
(本题满分16分)本题共有2个小题，第1小题满分6分，第2小题满分10分．
已知两点
、
，点
是直角坐标平面上的动点，若将点
的横坐标保持不变、纵坐标扩大到
倍后得到点
满足
．
(1) 求动点所在曲线
的轨迹方程；
(2)(理科)过点
作斜率为
的直线
交曲线于
两点，且满足
，又点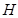
关于原点O的对称点为点
，试问四点
是否共圆，若共圆，求出圆心坐标和半径；若不共圆，请说明理由．
(文科)过点作斜率为的直线交曲线于两点，且满足(O为坐标原点)，试判断点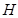是否在曲线上，并说明理由．
查看习题详情和答案>>
（本题满分16分）
函数f(x)＝x3＋3ax2＋3bx＋c在x＝2处有极值，其图象在x＝1处的切线平行于直线3x＋y＋2＝0．
（1）求a，b的值； （2）求函数的极大值与极小值的差．
查看习题详情和答案>>
，
=（1，2）．
，求tan
的值； （２）若
，
，求
．
在R上是增函数，求实数
的取值范围；
时，函数
，使得关于
的方程
有三个不相等的实数根，求实数
的取值范围．
．
在R上是增函数，求实数
的取值范围；
时，函数
，使得关于
的方程
有三个不相等的实数根，求实数
的取值范围．