摘要： 甲.乙两人各进行3次射击.甲每次击中目标的概率为.乙每次击中目标的概率为. (1)求乙至多击中目标2次的概率 (2)求甲恰好比乙多击中目标2次的概率 记甲击中目标的次数为ξ.求ξ的概率分布及数学期望Eξ.
网址：http://m.1010jiajiao.com/timu_id_3952238[举报]
甲、乙两人各进行3次射击，甲每次击中目标的概率为
，乙每次击中目标的概率
，
（Ⅰ）记甲击中目标的次数为X，求X的概率分布及数学期望；
（Ⅱ）求甲恰好比乙多击中目标2次的概率． 查看习题详情和答案>>
| 1 |
| 2 |
| 2 |
| 3 |
（Ⅰ）记甲击中目标的次数为X，求X的概率分布及数学期望；
（Ⅱ）求甲恰好比乙多击中目标2次的概率． 查看习题详情和答案>>
甲、乙两人各进行3次射击，甲每次击中目标的概率为
，乙每次击中目标的概率为
，两人间每次射击是否击中目标互不影响．
（1）求乙至多击中目标2次的概率；
（2）求甲恰好比乙多击中目标1次的概率．
查看习题详情和答案>>
| 2 |
| 3 |
| 1 |
| 2 |
（1）求乙至多击中目标2次的概率；
（2）求甲恰好比乙多击中目标1次的概率．
甲、乙两人各进行3次射击，甲每次击中目标的概率是
，乙每次击中目标的概率是
．
（1）求甲至多击中2次，且乙至少击中2次的概率；
（2）若规定每击中一次得3分，未击中得-1，求乙所得分数ξ的概率和数学期望．
查看习题详情和答案>>
| 1 |
| 2 |
| 2 |
| 3 |
（1）求甲至多击中2次，且乙至少击中2次的概率；
（2）若规定每击中一次得3分，未击中得-1，求乙所得分数ξ的概率和数学期望．
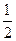，乙每次击中目标的概率
，
，乙每次击中目标的概率为
.
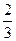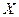，求