摘要：如图.已知四棱锥的底面是菱形, 平面, 点为的中点. (Ⅰ)求证:平面; (Ⅱ)求证:平面. 设函数...且以为最小正周期． (1)求, (2)求的解析式, (3)已知.求的值． 甲.乙两人各进行3次射击.甲每次击中目标的概率为.乙每次击中目标的概率为. (1)求乙至多击中目标2次的概率, (2)求甲恰好比乙多击中目标2次的概率. 已知等差数列满足:..的前项和为 (Ⅰ)求及, (Ⅱ)令().求数列的前项和为 已知中心在坐标原点O的椭圆C经过点A为其右焦点. (1)求椭圆C的方程, (2)是否存在平行于OA的直线.使得直线与椭圆C有公共点.且直线OA与的距离等于4?若存在.求出直线的方程,若不存在.请说明理由. 设函数在及时取得极值． (Ⅰ)求a.b的值, (Ⅱ)若对于任意的.都有成立.求c的取值范围．
网址：http://m.1010jiajiao.com/timu_id_3947599[举报]
(本题满分10分)
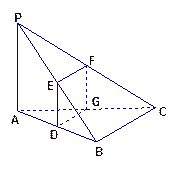
如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.
(1)求异面直线AF与BG所成的角的大小；
(2)求平面APB与平面CPD所成的锐二面角的余弦值
查看习题详情和答案>>
(本题满分10分)
如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.
(1)求异面直线AF与BG所成的角的大小；
(2)求平面APB与平面CPD所成的锐二面角的余弦值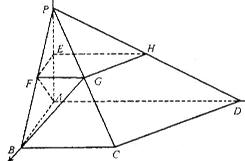
(本题满分10分)
如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.
(1)求异面直线AF与BG所成的角的大小；
(2)求平面APB与平面CPD所成的锐二面角的余弦值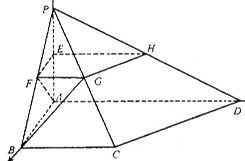
如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.
(1)求异面直线AF与BG所成的角的大小；
(2)求平面APB与平面CPD所成的锐二面角的余弦值
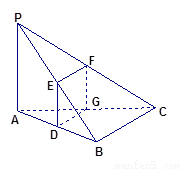如图,已知三棱锥P—ABC中，PA⊥平面ABC，设AB、PB、PC的中点分别为D、E、F，