摘要:已知函数f(x)=-x3+3x2+9x+a. (1)求f(x)的单调区间, (2)若f(x)在区间[-2,2]上的最大值为20.求函数f(x)在该区间上的最小值. 解:(1)f′(x)=-3x2+6x+9.令f′(x)<0.解得x<-1或x>3.所以函数f(x)的单调递减区间为, 令f′(x)>0.解得-1<x<3.所以函数f(x)的单调递增区间为. (2)因为f(-2)=8+12-18+a=2+a.f(2)=-8+12+18+a=22+a. 所以f(2)>f(-2). 因为在区间上.f′(x)>0.所以f(x)在上单调递增. 又由于f(x)在上单调递减. 因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值. 于是有22+a=20.解得a=-2. 故f(x)=-x3+3x2+9x-2. 因此f(-1)=-7.即函数f(x)在区间[-2,2]上的最小值为-7.
网址:http://m.1010jiajiao.com/timu_id_3946508[举报]
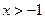 ,证明:
,证明: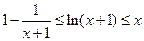 .
.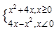 (1)作出函数
(1)作出函数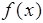 的图像简图,并指出函数
的图像简图,并指出函数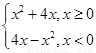
 的图像简图,并指出函数
的图像简图,并指出函数