题目内容
(本小题满分12分)已知函数f(x)=ln(x+1)-x.
⑴求函数f(x)的单调递减区间;
⑵若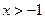 ,证明:
,证明: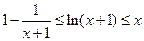 .
.
解:⑴函数f(x)的定义域为 .
. =
= -1=-
-1=- 。由
。由 <0及x>-1,得x>0.∴当x∈(0,+∞)时,f(x)是减函数,即f(x)的单调递减区间为(0,+∞).
<0及x>-1,得x>0.∴当x∈(0,+∞)时,f(x)是减函数,即f(x)的单调递减区间为(0,+∞).
⑵证明:由⑴知,当x∈(-1,0)时, >0,当x∈(0,+∞)时,
>0,当x∈(0,+∞)时, <0,
<0,
因此,当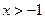 时,
时, ≤
≤ ,即
,即 ≤0∴
≤0∴ .
.
令 ,则
,则 =
= .
.
∴当x∈(-1,0)时, <0,当x∈(0,+∞)时,
<0,当x∈(0,+∞)时, >0.
>0.
∴当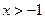 时,
时, ≥
≥ ,即
,即 ≥0,∴
≥0,∴ .
.
综上可知,当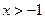 时,有
时,有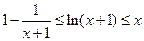 .
.
解析

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目