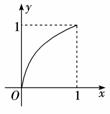
摘要:已知定义在区间[0,1]上的函数y=f(x)的图象如图所示.对于满足0<x1<x2<1的任意x1.x2.给出下列结论: ①f(x2)-f(x1)>x2-x1, ②x2f(x1)>x1f(x2), ③<f (). 其中正确结论的序号是 (把所有正确结论的序号都填上). 解析:由f(x2)-f(x1)>x2-x1.可得>1.即两点(x1.f(x1))与(x2.f(x2))连线的斜率大于1.显然①不正确,由x2f(x1)>x1f(x2)得>.即表示两点(x1.f(x1)).(x2.f(x2))与原点连线的斜率的大小.可以看出结论②正确,结合函数图象.容易判断③的结论是正确的. 答案:②③
网址:http://m.1010jiajiao.com/timu_id_3946436[举报]
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
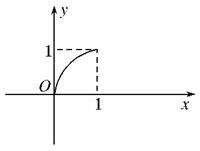
①f(x2)-f(x1)>x2-x1;
②x2f(x1)>x1f(x2);
③![]() <f
<f![]() .
.
其中正确结论的序号是___: _____.(把所有正确结论的序号都填上)
查看习题详情和答案>>已知定义在区间[0,1]上的函数y=f(x)的图象如右图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
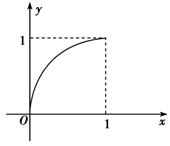
①f(x2)-f(x1)>x2-x1;
②x2f(x1)>x1f(x2);
③<f.
其中正确结论的序号是________.(把所有正确结论的序号都填上)
查看习题详情和答案>>
已知定义在区间[0,1]上的函数y=f(x),图象如图所示.对满足0<x1<x2<1的任意x1,x2,给出下列结论:
①f(x1)-f(x2)>x1-x2;②x2f(x1)>x1f(x2);③![]() <f(
<f(![]() ).
).
其中正确结论的序号是________.(把所有正确结论的序号都填上)