摘要:12.设f(x)=|x2-a2|dx. (1)当0≤a≤1与a>1时.分别求f(a), (2)当a≥0时.求f(a)的最小值. 解:(1)0≤a≤1时. f(a)=|x2-a2|dx =(a2-x2)dx+(x2-a2)dx =(a2x-x3)+(-a2x) =a3-a3-0+0+-a2-+a3 =a3-a2+. 当a>1时. f(a)=(a2-x2)dx =(a2x-x3) =a2-. ∴f(a)= (2)当a>1时.由于a2-在[1.+∞)上是增函数.故f(a)在[1.+∞)上的最小值是f(1)=1-=. 当a∈[0,1]时.f′(a)=4a2-2a=2a(2a-1). 由f′(a)>0知:a>或a<0. 故在[0.]上递减.在[.1]上递增. 因此在[0,1]上.f(a)的最小值为f()=. 综上可知.f(x)在[0.+∞)上的最小值为.
网址:http://m.1010jiajiao.com/timu_id_3946382[举报]
设f(x)=x2+bx+c,且f(-1)=f(3),则 ( )
A.f(1)>c>f(-1) B.f(1)<c<f(-1)
C.f(1)>f(-1)>c D.f(1)<f(-1)<c
查看习题详情和答案>>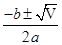 ,得x1=3,x2=-1.
,得x1=3,x2=-1.