题目内容
设f(x)=x2-2ax+2.当x∈[-1,+∞)时,f(x)≥a恒成立,求实数a的取值范围.
答案:
解析:
解析:
|
当a≤-1时,f(x)min=f(-1)=3+2a, 当x∈[-1,+∞),f(x)≥a恒成立f(x)min≥a, 即3+2a≥a 故此时-3≤a≤-1. 当a>-1时,f(x)min=f(a)=a2-2a2+2=2-a2, 当x∈[-1,+∞),f(x)≥a恒成立f(x)min≥a, 即2-a2≥a 故此时-1<a≤1. 综上所得,实数a的取值范围为-3≤a≤1. |

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
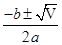 ,得x1=3,x2=-1.
,得x1=3,x2=-1. 上是减函数,则实数a的范围是
上是减函数,则实数a的范围是 上是减函数,则实数a的范围是( )
上是减函数,则实数a的范围是( )