摘要：12．＝m的图象与h(x)＝+2的图象关于点A(0,1)对称． (1)求m的值, +在(0,2]上是减函数.求实数a的取值范围． [解析] 图象上一点.点P关于A(0,1)的对称点为Q(x0.y0).则x0＝-x.y0＝2-y. ∴2-y＝m.∴y＝m+2.从而m＝. ＝+＝. 设0<x1<x2≤2. 则g(x1)-g(x2)＝- ＝(x1-x2)+(a+1)· ＝(x1-x2)·>0. 并且在x1.x2∈(0,2]上恒成立. ∴x1x2-(a+1)<0.∴1+a>x1x2,1+a≥4.∴a≥3.
网址：http://m.1010jiajiao.com/timu_id_3942711[举报]
已知函数f(x)＝m(
)的图象与函数h(x)＝
(
)的图象关于点A(0，1)对称．
(1)求m的值．
(2)若g(x)＝f(x)＋
在区间(0，2]上为减函数，求实数a的取值范围．
已知函数f(x)＝m(x＋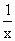
)的图象与函数h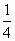(x)＝
(x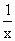＋)＋2的图象关于点A(0，1)对称
(1)求m的值；
(2)若g(x)＝f(x)＋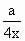
在区间(0，2]上为减函数，求实数a的取值范围．
21、已知函数f(x)＝lnx，g(x)＝－
ax2＋bx，a≠0。
ax2＋bx，a≠0。 （Ⅰ）若b＝2，且h(x)＝f(x)－g(x)存在单调递减区间，求a的取值范围；
（Ⅱ）设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q，过线段PQ的中点作x轴的垂线分别交C1，C2于点M、N，证明C1在点M处的切线与C2在点N处的切线不平行。
查看习题详情和答案>>
ax2＋bx(a≠0)．
(x)＝e2x＋bex，x∈[0，ln2]，求函数
ax2＋bx(a≠0)．