摘要:22.解:(1)∵椭圆长轴长为 又∵椭圆过点.代入椭圆方程得 ∴椭圆方程为 即 ----3分 (2)∵直线且斜率为k. 设直线方程为 由 设∵线段AB中点的横坐标是 则 即 ----7分 (3)假设在x轴上存在点. 使是与k无关的常数. 由 设 则 ----9分 是与k无关的常数.设常数为t. 则 ----12分 整理得对任意的k恒成立 .解得 即在x轴上存在点. 使是与k无关的常数. ----14分
网址:http://m.1010jiajiao.com/timu_id_3936859[举报]
定义:关于x的不等式|x-A|<B的解集叫A的B邻域.已知a+b-2的a+b邻域为区间(-2,8),其中a、b分别为椭圆
+
=1的长半轴和短半轴.若此椭圆的一焦点与抛物线y2=4
x的焦点重合,则椭圆的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
(1)若椭圆的方程是:
+
=1(a>b>0),它的左、右焦点依次为F1、F2,P是椭圆上异于长轴端点的任意一点.在此条件下我们可以提出这样一个问题:“设△PF1F2的过P角的外角平分线为l,自焦点F2引l的垂线,垂足为Q,试求Q点的轨迹方程?”
对该问题某同学给出了一个正确的求解,但部分解答过程因作业本受潮模糊了,我们在
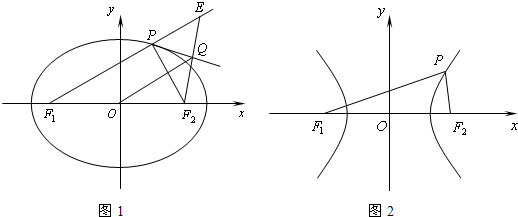
这些模糊地方划了线,请你将它补充完整.
解:延长F2Q 交F1P的延长线于E,据题意,
E与F2关于l对称,所以|PE|=|PF2|.
所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|= ,
在△EF1F2中,显然OQ是平行于EF1的中位线,
所以|OQ|=
|EF1|= ,
注意到P是椭圆上异于长轴端点的点,所以Q点的轨迹是 ,
其方程是: .
(2)如图2,双曲线的方程是:
-
=1(a,b>0),它的左、右焦点依次为F1、F2,P是双曲线上异于实轴端点的任意一点.请你试着提出与(1)类似的问题,并加以证明.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
对该问题某同学给出了一个正确的求解,但部分解答过程因作业本受潮模糊了,我们在
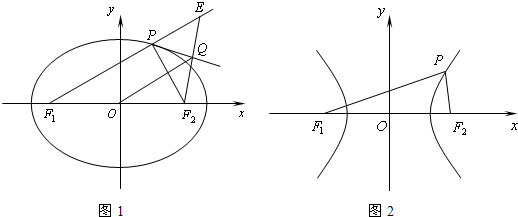
这些模糊地方划了线,请你将它补充完整.
解:延长F2Q 交F1P的延长线于E,据题意,
E与F2关于l对称,所以|PE|=|PF2|.
所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|=
在△EF1F2中,显然OQ是平行于EF1的中位线,
所以|OQ|=
| 1 |
| 2 |
注意到P是椭圆上异于长轴端点的点,所以Q点的轨迹是
其方程是:
(2)如图2,双曲线的方程是:
| x2 |
| a2 |
| y2 |
| b2 |
定义:关于x的不等式|x-A|<B的解集叫A的B邻域.
已知a+b-2的a+b邻域为区间(-2,8),其中a、b分别为椭圆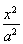 +
+ =1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4
=1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4 x的焦点重合,则椭圆的方程为( )
x的焦点重合,则椭圆的方程为( )
(A)  +
+ =1 (B)
=1 (B) 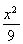 +
+ =1
=1
(C) 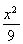 +
+ =1 (D)
=1 (D)  +
+ =1
=1
查看习题详情和答案>>
定义:关于x的不等式|x-A|<B的解集叫A的B邻域.已知a+b-2的a+b邻域为区间(-2,8),其中a、b分别为椭圆
+
=1的长半轴和短半轴.若此椭圆的一焦点与抛物线y2=4
x的焦点重合,则椭圆的方程为( )
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A.
| B.
| C.
| D.
|
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点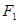 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.
【解析】(1)中利用点F1到直线x=- 的距离为
的距离为 可知-
可知- +
+ =
= .得到a2=4而c=
.得到a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
得到椭圆的方程。(2)中,利用 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。
解:(1)∵F1到直线x=- 的距离为
的距离为 ,∴-
,∴- +
+ =
= .
.
∴a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为 +y2=1.……4分
+y2=1.……4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知
 ,
,
∴ ……6分
……6分
∵A、B在椭圆 +y2=1上,
+y2=1上,
∴ ……10分
……10分
∴l的斜率为 =
= .
.
∴l的方程为y= (x-
(x- ),即
),即 x-y-
x-y- =0.
=0.
查看习题详情和答案>>