题目内容
设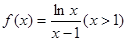
(Ⅰ)判断函数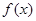 的单调性;
的单调性;
(Ⅱ)是否存在实数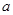 、使得关于
、使得关于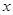 的不等式
的不等式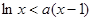 在(1,
在(1,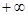 )上恒成立,若存在,求出
)上恒成立,若存在,求出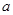 的取值范围,若不存在,试说明理由.
的取值范围,若不存在,试说明理由.
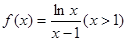
(Ⅰ)判断函数
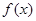 的单调性;
的单调性;(Ⅱ)是否存在实数
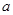 、使得关于
、使得关于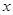 的不等式
的不等式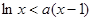 在(1,
在(1,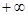 )上恒成立,若存在,求出
)上恒成立,若存在,求出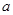 的取值范围,若不存在,试说明理由.
的取值范围,若不存在,试说明理由.(1)函数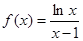 在
在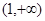 上为减函数. (2)
上为减函数. (2)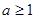
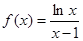 在
在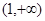 上为减函数. (2)
上为减函数. (2)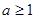
本试题主要是考查了导数在研究函数中的运用。
(1)利用已知的函数,得到其导函数,然后再对导函数的分母分析,求导,得到原函数的单调性的判定问题。
(2)因为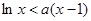 在
在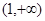 上恒成立,即
上恒成立,即 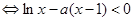 在
在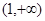 上恒成立,
上恒成立,
那么构造函数的思想,得到函数的最大值小于零即可。分析证明
(1)∵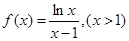 ∴
∴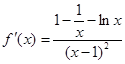 , 设
, 设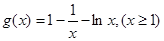 .
.
∴ ,∴
,∴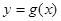 在
在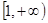 上为减函数. …… 4分
上为减函数. …… 4分
∴ ,∴
,∴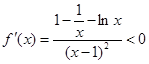
∴函数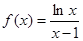 在
在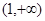 上为减函数. …… 6分
上为减函数. …… 6分
(2)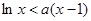 在
在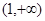 上恒成立,
上恒成立,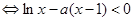 在
在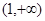 上恒成立,
上恒成立,
设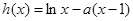 ,则
,则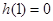 ,∴
,∴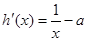 , …… 7分
, …… 7分
若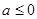 显然不满足条件, 若
显然不满足条件, 若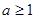 ,则
,则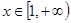 时,
时, 恒成立,∴
恒成立,∴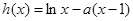 在
在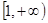 上为减函数∴
上为减函数∴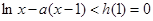 在
在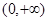 上恒成立,∴
上恒成立,∴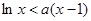 在
在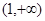 上恒成立, …… 10分
上恒成立, …… 10分
若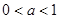 ,则
,则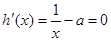 时,
时, ,∴
,∴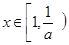 时
时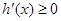 ,∴
,∴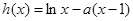 在
在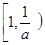 上为增函数,当
上为增函数,当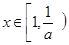 时,
时, ,
,
不能使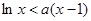 在
在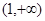 上恒成立,∴
上恒成立,∴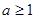
(1)利用已知的函数,得到其导函数,然后再对导函数的分母分析,求导,得到原函数的单调性的判定问题。
(2)因为
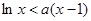 在
在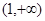 上恒成立,即
上恒成立,即 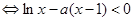 在
在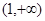 上恒成立,
上恒成立,那么构造函数的思想,得到函数的最大值小于零即可。分析证明
(1)∵
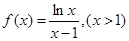 ∴
∴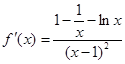 , 设
, 设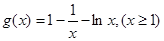 .
.∴
 ,∴
,∴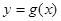 在
在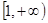 上为减函数. …… 4分
上为减函数. …… 4分∴
 ,∴
,∴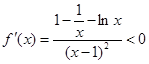
∴函数
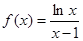 在
在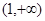 上为减函数. …… 6分
上为减函数. …… 6分(2)
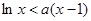 在
在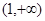 上恒成立,
上恒成立,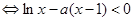 在
在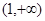 上恒成立,
上恒成立,设
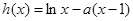 ,则
,则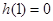 ,∴
,∴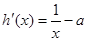 , …… 7分
, …… 7分若
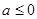 显然不满足条件, 若
显然不满足条件, 若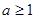 ,则
,则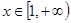 时,
时, 恒成立,∴
恒成立,∴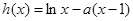 在
在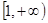 上为减函数∴
上为减函数∴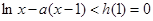 在
在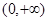 上恒成立,∴
上恒成立,∴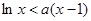 在
在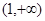 上恒成立, …… 10分
上恒成立, …… 10分若
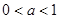 ,则
,则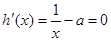 时,
时, ,∴
,∴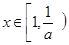 时
时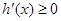 ,∴
,∴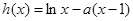 在
在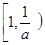 上为增函数,当
上为增函数,当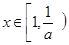 时,
时, ,
,不能使
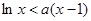 在
在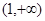 上恒成立,∴
上恒成立,∴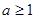

练习册系列答案
相关题目
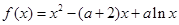 ,其中常数
,其中常数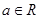 .
.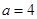 时,求函数
时,求函数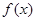 的极值点;
的极值点;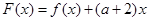 ,若函数
,若函数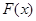 在区间
在区间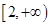 上单调递增,求
上单调递增,求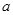 的取值范围;
的取值范围;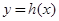 在点
在点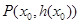 处的切线方程为
处的切线方程为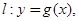 当
当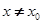 时,若
时,若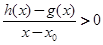 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数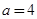 时,函数
时,函数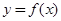 是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.
是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.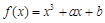 .
.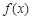 在
在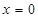 处取得极值为
处取得极值为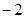 ,求
,求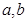 的值;
的值;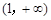 上是增函数,求实数
上是增函数,求实数 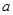 的取值范围.
的取值范围.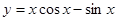 在下列哪个区间内是增函数( )
在下列哪个区间内是增函数( )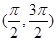
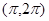
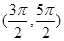
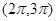
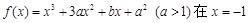 时的极值为0.
时的极值为0.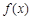 的单调区间.
的单调区间.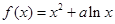
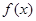 +
+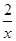 在
在 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.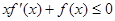 ,对任意正数a,b,若a<b,
,对任意正数a,b,若a<b,



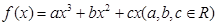 ,
,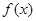 过点
过点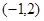 且在点
且在点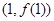 处的切线方程是
处的切线方程是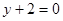 ,求函数
,求函数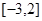 上任意两个自变量的值
上任意两个自变量的值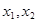 ,都有
,都有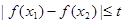 ,求实数
,求实数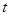 的最小值。
的最小值。