摘要：直线和平面所成的角 (1)定义 和平面所成的角有三种: (i)垂线 面所成的角 的一条斜线和它在平面上的射影所成的锐角.叫做这条直线和这个平面所成的角. (ii)垂线与平面所成的角 直线垂直于平面.则它们所成的角是直角. (iii)一条直线和平面平行.或在平面内.则它们所成的角是0°的角. (2)取值范围: (3)求解方法 ①作出斜线在平面上的射影.找到斜线与平面所成的角θ. ②解含θ的三角形.求出其大小.
网址：http://m.1010jiajiao.com/timu_id_3933752[举报]
定义：对于映射f：A→B，如果A中的不同元素有不同的象，且B中的每一个元素都有原象，则称f：A→B为一一映射．如果存在对应关系φ，使A到B成为一一映射，则称A和B具有相同的势．给出下列命题：
①A={奇数}，B={偶数}，则A和B 具有相同的势；
②A是直角坐标系平面内所有点形成的集合，B是复数集，则A和B 不具有相同的势；
③若A={
，
}，其中
，
是不共线向量，B={
|
与
，
共面的任意向量}，则A和B不可能具有相同的势；
④若区间A=（-1，1），B=（-∞，+∞），则A和B具有相同的势．
其中真命题为
查看习题详情和答案>>
①A={奇数}，B={偶数}，则A和B 具有相同的势；
②A是直角坐标系平面内所有点形成的集合，B是复数集，则A和B 不具有相同的势；
③若A={
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
④若区间A=（-1，1），B=（-∞，+∞），则A和B具有相同的势．
其中真命题为
①③④
①③④
．
定义：对于映射f：A→B，如果A中的不同元素有不同的象，且B中的每一个元素都有原象，则称f：A→B为一一映射．如果存在对应关系φ，使A到B成为一一映射，则称A和B具有相同的势．给出下列命题：
①A={奇数}，B={偶数}，则A和B 具有相同的势；
②A是直角坐标系平面内所有点形成的集合，B是复数集，则A和B 不具有相同的势；
③若A={
，
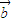}，其中
，
是不共线向量，B={
|
与
，
共面的任意向量}，则A和B不可能具有相同的势；
④若区间A=（-1，1），B=（-∞，+∞），则A和B具有相同的势．
其中真命题为 ． 查看习题详情和答案>>
①A={奇数}，B={偶数}，则A和B 具有相同的势；
②A是直角坐标系平面内所有点形成的集合，B是复数集，则A和B 不具有相同的势；
③若A={
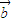，}，其中，是不共线向量，B={|与，共面的任意向量}，则A和B不可能具有相同的势；④若区间A=（-1，1），B=（-∞，+∞），则A和B具有相同的势．
其中真命题为 ． 查看习题详情和答案>>
，其中 
是不共线向量，B={ 
|
与
共面的任意向量}，则A和B不可能具有相同的势； 
，
}，其中
|