摘要：公式组一 公式组二: , 公式组三 , , , 常用数据: 的三角函数值 , , 注: ⑴以上公式务必要知道其推导思路.从而清晰地“看出 它们之间的联系.它们的变化形式.如 等. 从而可做到:正用.逆用.变形用自如使用各公式. ⑵三角变换公式除用来化简三角函数式外.还为研究三角函数图象及性质做准备. ⑶三角函数恒等变形的基本策略. ①常值代换:特别是用“1 的代换.如1=cos2θ+sin2θ=tanx·cotx=tan45°等. ②项的分拆与角的配凑.如分拆项:; 配凑角:.. ..等. ③降次与升次.即倍角公式降次与半角公式升次. ④化弦(切)法.将三角函数利用同角三角函数基本关系化成弦(切). ⑤引入辅助角.asinθ+bcosθ=sin(θ+).这里辅助角所在象限由a.b的符号确定.角的值由tan=确定. 典型例题 例1.同角三角函数的基本关系 已知.求． 变式1:已知.<x<.求的值．1/2 变式2.化简: sin10 例2.两角和与差及二倍角的三角函数 已知..求.的值．,-7 变式1.已知tanα.tanβ是方程两根.且α.β.则α+β等于或 变式2. 的值是4 变式3. 设,若则= 变式4. 变式5:在中.已知..． (Ⅰ)求的值, (Ⅱ)求的值． 变式6:在中..． (Ⅰ)求角的大小,135 (Ⅱ)若最大边的边长为.求最小边的边长． 变式7:已知.且, (Ⅰ)求的值,- (Ⅱ)求. 实战训练1．是第四象限角..则
网址：http://m.1010jiajiao.com/timu_id_3929336[举报]
| 某学校高三年级有学生1 000名，经调查研究，其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼（称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学， (Ⅰ)求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学； (Ⅱ)测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如下图： | ||||||||||||||||
 | ||||||||||||||||
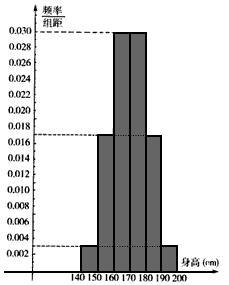| (ⅰ)统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170)的中点值为165）作为代表。据此，计算这100名学生身高数据的期望μ及标准差σ（精确到0.1）： (ⅱ)若总体服从正态分布，以样本估计总体，据此，估计该年级身高在(158.6，181.4)范围中的学生的人数； (Ⅲ)如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表： | ||||||||||||||||
|
体育锻炼与身高达标2×2列联表 | ||||||||||||||||
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系？ 参考公式：  ，参考数据： | ||||||||||||||||
 |
（本小题满分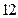
分）某学校高三年级有学生1000名，经调查研究,其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼(称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
(Ⅱ) 测得该年级所抽查的100名同学身高(单位：厘米) 频率分布直方图如右图：
(ⅰ) 统计方法中，同一组数据常用该组区间的中点值（例如区间
的中点值为165）作为代表．据此，计算这100名学生身高数据的期望
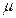及标准差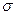
(精确到0.1)；
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在
范围中的学生的人数．
(Ⅲ) 如果以身高达170cm作为达标的标准，对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| | 身高达标 | 身高不达标 | 总计 |
| 积极参加体育锻炼 | 40 | | |
| 不积极参加体育锻炼 | | 15 | |
| 总计 | | | 100 |
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K
=
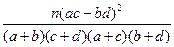,参考数据:P(K k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
（本小题满分
分）某学校高三年级有学生1000名，经调查研究,其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼(称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学.
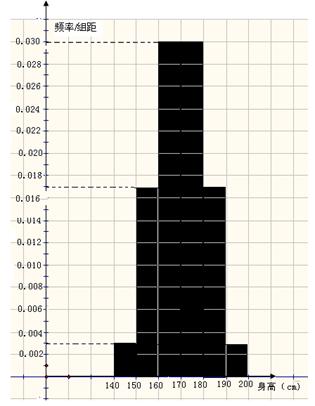
(Ⅰ)求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
(Ⅱ) 测得该年级所抽查的100名同学身高(单位：厘米) 频率分布直方图如右图：
(ⅰ) 统计方法中，同一组数据常用该组区间的中点值（例如区间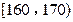
的中点值为165）作为代表．据此，计算这100名学生身高数据的期望
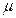及标准差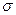
(精确到0.1)；
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在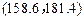
范围中的学生的人数．
(Ⅲ) 如果以身高达170cm作为达标的标准，对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
(ⅰ)完成上表；
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K
=
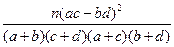,参考数据:
分）某学校高三年级有学生1000名，经调查研究,其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼(称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学.(Ⅰ)求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
(Ⅱ) 测得该年级所抽查的100名同学身高(单位：厘米) 频率分布直方图如右图：
(ⅰ) 统计方法中，同一组数据常用该组区间的中点值（例如区间
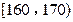的中点值为165）作为代表．据此，计算这100名学生身高数据的期望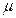及标准差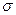(精确到0.1)；(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在
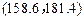范围中的学生的人数．(Ⅲ) 如果以身高达170cm作为达标的标准，对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| | 身高达标 | 身高不达标 | 总计 |
| 积极参加体育锻炼 | 40 | | |
| 不积极参加体育锻炼 | | 15 | |
| 总计 | | | 100 |
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K
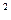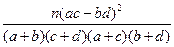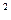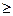=,参考数据:P(K k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
某学校高三年级有学生1000名，经调查研究，其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼（称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学．
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表
（ⅰ）完成上表；
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K2=
，参考数据：
查看习题详情和答案>>
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表
| 身高达标 | 身高不达标 | 总计 | |
| 积极参加体育锻炼 | 40 | ||
| 不积极参加体育锻炼 | 15 | ||
| 总计 | 100 |
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K2=
| π(ac-bd)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P（K2≥k） | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
某学校高三年级有学生1000名，经调查研究，其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼（称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学．
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表
（ⅰ）完成上表；
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K2=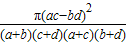
，参考数据：
查看习题详情和答案>>
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表
| 身高达标 | 身高不达标 | 总计 | |
| 积极参加体育锻炼 | 40 | ||
| 不积极参加体育锻炼 | 15 | ||
| 总计 | 100 |
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K2=
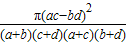，参考数据：| P（K2≥k） | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看习题详情和答案>>