摘要:20. 在一条笔直的工艺流水线上有个工作台.将工艺流水线用如图所示的数轴表示.各工作台的坐标分别为...每个工作台上有若干名工人.现要在与之间修建一个零件供应站.使得各工作台上的所有工人到供应站的距离之和最短. (Ⅰ)若每个工作台上只有一名工人.试确定供应站的位置, (Ⅱ)设工作台从左到右的人数依次为...试确定供应站的位置.并求所有工人到供应站的距离之和的最小值. 图5 [解析]设供应站坐标为.各工作台上的所有工人到供应站的距离之和为. (Ⅰ)由题设知..所以 --分 . --分 故当时.取最小值.此时供应站的位置为. --分 (Ⅱ)由题设知..所以各工作台上的所有工人到供应站的距离之和为 . --分 且 --分 因此.函数在区间上是减函数.在区间上是常数.故供应站位置位于区间上任意一点时.均能使函数取得最小值.且最小值为.. --分 题目:已知集合是同时满足下列两个性质的函数的全体: ①在其定义域上是单调增函数或单调减函数,②在的定义域内存在区间.使得在上的值域是. (Ⅰ)判断函数是否属于集合?并说明理由.若是.请找出区间, (Ⅱ)若函数.求实数的取值范围. [解析](Ⅰ)的定义域是. .在上是单调减函数. 则在上的值域是. 由 解得:或或 函数属于集合.且这个区间是. --5分 (Ⅱ)设.则易知是定义域上的增函数. .存在区间.满足.. 即方程在内有两个不等实根. --7分 方程在内有两个不等实根.等价于方程在内有两个不等实根. 即方程在内有两个不等实根. --9分 根据一元二次方程根的分布有 --12分 解得. 因此.实数的取值范围是. --13分
网址:http://m.1010jiajiao.com/timu_id_3926237[举报]
(本小题满分13分)
在一条笔直的工艺流水线上有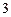 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图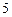 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为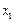 ,
, ,
,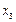 ,每个工作台上有若干名工人.现要在
,每个工作台上有若干名工人.现要在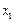 与
与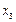 之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(Ⅰ)若每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)设工作台从左到右的人数依次为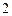 ,
,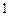 ,
,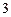 ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
图5
(本小题满分13分)
在一条笔直的工艺流水线上有 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,每个工作台上有若干名工人.现要在
,每个工作台上有若干名工人.现要在 与
与 之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(Ⅰ)若每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)设工作台从左到右的人数依次为 ,
, ,
, ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.

图5
查看习题详情和答案>>
 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,
, ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短. ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置; ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为 ,
, ,
, ,
,
 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,
, ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短. ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置; ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为 ,
, ,
, ,
,