摘要: 点到直线的距离公式:设已知点P(x0.y0).直线l的方程为:Ax+By+C=0. 例1. 在等腰Rt△ABC中.∠C=90°.直角边BC在直线2x+3y-6=0上.顶点A(5.4).求AB和AC所在的直线方程. 解析: 例2. 解: 例3. 通过A.求底边所在的直线方程. 解析:根据等腰三角形的两个底角相等.由此等量关系.根据到角公式即可求出底边的斜率. 解:设底边的斜率为k 例4. 与反射光线所在的直线方程. 分析:根据入射角等于反射角知识.可知:点A的对称点A'应在反射光线上.连结A'B交已知直线于D.则AD为入射线.则任务为求A'B和AD的方程. 解: 例5. 证明:三点A共线. 分析:可采取其中一点到过另两点的直线的距离为0来证明. 证明: 说明:证三点共线: [模拟试题]
网址:http://m.1010jiajiao.com/timu_id_3922963[举报]
 如图,类比直线方程的截距式和点到直线的距离公式,则点H(4,2,1)到平面ABC的距离是
如图,类比直线方程的截距式和点到直线的距离公式,则点H(4,2,1)到平面ABC的距离是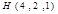 到平面
到平面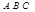 的距离是 .
的距离是 .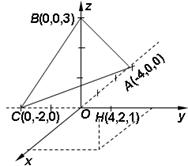
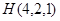 到平面
到平面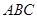 的距离是 .
的距离是 .
 、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程. ,化为普通方程;(Ⅱ)利用点到直线的距离公式表示出距离,求最值.
,化为普通方程;(Ⅱ)利用点到直线的距离公式表示出距离,求最值.