摘要:20.已知.且.求证:. 设...易知. ------2分 由知. ------4分 所以, ------6分 又 . 所以.故. ------13分 所以 ------14分
网址:http://m.1010jiajiao.com/timu3_id_4473420[举报]
(本小题共14分)已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .
.
(Ⅰ)判断函数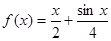 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为
的定义域为 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;
(Ⅲ)对任意 ,且
,且 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
,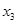 ,当
,当 ,且
,且 时,
时, .
.
查看习题详情和答案>>
(19)(本小题共14分)
已知抛物线![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 过点
过点![]() 交抛物线于
交抛物线于![]() 两点.
两点.
(Ⅰ)证明:直线![]() 的斜率互为相反数;
的斜率互为相反数;
(Ⅱ)求![]() 面积的最小值;
面积的最小值;
(Ⅲ)当点![]() 的坐标为
的坐标为![]() ,且
,且![]() .根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):
.根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):
① 直线![]() 的斜率是否互为相反数?
的斜率是否互为相反数?
② ![]() 面积的最小值是多少?
面积的最小值是多少?
(19)(本小题共14分)
已知抛物线![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 过点
过点![]() 交抛物线于
交抛物线于![]() 两点.
两点.
(Ⅰ)证明:直线![]() 的斜率互为相反数;
的斜率互为相反数;
(Ⅱ)求![]() 面积的最小值;
面积的最小值;
(Ⅲ)当点![]() 的坐标为
的坐标为![]() ,且
,且![]() .根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):
.根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):
① 直线![]() 的斜率是否互为相反数?
的斜率是否互为相反数?
② ![]() 面积的最小值是多少?
面积的最小值是多少?
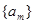 是首项为
是首项为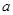 ,公差为
,公差为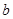 的等差数列,
的等差数列,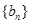 是首项为
是首项为 ,其中
,其中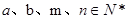 .
.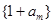 与数列
与数列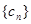 ,求数列
,求数列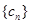 的通项公式;
的通项公式;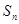 ,求证:
,求证: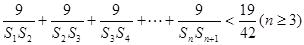 .
.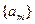 是首项为
是首项为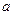 ,公差为
,公差为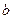 的等差数列,
的等差数列,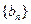 是首项为
是首项为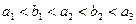 ,其中
,其中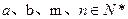 .
.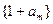 与数列
与数列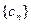 ,求数列
,求数列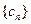 的通项公式;
的通项公式;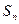 ,求证:
,求证: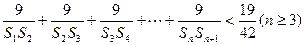 .
.