摘要:对任意正整数与., 对任意正整数., 对任意正整数与.当时. 求证:恰有一个函数满足上述三个性质.并求出这个函数.
网址:http://m.1010jiajiao.com/timu3_id_4470369[举报]
对于任意的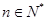 (
(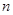 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前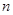 项和等于该数列的前
项和等于该数列的前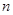 项之积,则称该数列为
项之积,则称该数列为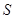 型数列。
型数列。
(1)若数列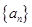 是首项
是首项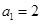 的
的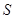 型数列,求
型数列,求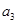 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是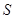 型数列;
型数列;
(3)若数列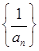 是
是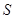 型数列,且
型数列,且 试求
试求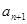 与
与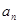 的递推关系,并证明
的递推关系,并证明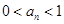 对
对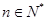 恒成立。
恒成立。
查看习题详情和答案>>
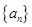 :
: 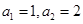 ,且对任意正整数
,且对任意正整数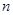 ,有
,有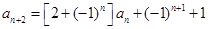 .
.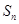 ;
; 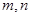 ,使得
,使得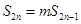 ?若存在,则求出所有的正整数对
?若存在,则求出所有的正整数对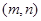 ;若不存在,则加以证明.
;若不存在,则加以证明.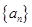 :
: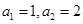 ,且对任意正整数
,且对任意正整数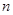 ,有
,有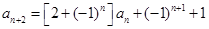 .
.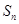 ;
;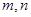 ,使得
,使得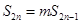 ?若存在,则求出所有的正整数对
?若存在,则求出所有的正整数对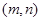 ;若不存在,则加以证明.
;若不存在,则加以证明. (
( 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前 型数列。
型数列。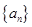 是首项
是首项 的
的 的值;
的值; 是
是 试求
试求 与
与 的递推关系,并证明
的递推关系,并证明 对
对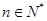 (
(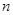 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前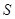 型数列。
型数列。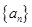 是首项
是首项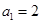 的
的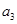 的值;
的值;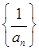 是
是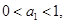 试求
试求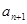 与
与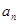 的递推关系,并证明
的递推关系,并证明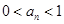 对
对