摘要:设函数的定义域.值域均为.的反函数为.且对于任意实数.均有.定义数列:. (1)求证:, (2)设求证:, 是否存在常数.同时满足:①当时.有,② 当.时.有成立.如果存在满足上述条件的实数.求出的值,如果不存在.证明你的结论.
网址:http://m.1010jiajiao.com/timu3_id_4470305[举报]
(本小题满分15分)
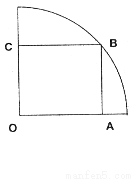
如图,在半径为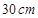 的
的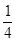 圆形(
圆形(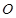 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料 ,其中点
,其中点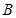 在圆上,点
在圆上,点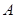 、
、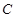 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮 卷成一个以
卷成一个以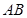 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长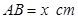 ,圆柱的体积为
,圆柱的体积为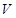
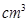 .
.
(1)写出体积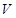 关于
关于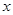 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当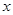 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积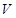 最大?最大体积是多少?
最大?最大体积是多少?
查看习题详情和答案>>
(本小题满分15分)
如图,在半径为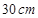 的
的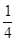 圆形(
圆形( 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料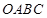 ,其中点
,其中点 在圆上,点
在圆上,点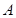 、
、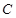 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮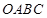 卷成一个以
卷成一个以 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长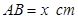 ,圆柱的体积为
,圆柱的体积为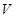
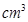 .
.
(1)写出体积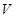 关于
关于 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积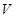 最大?最大体积是多少?
最大?最大体积是多少?
(本小题满分15分)
如图,在半径为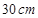 的
的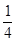 圆形(
圆形(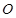 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料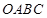 ,其中点
,其中点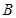 在圆上,点
在圆上,点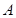 、
、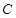 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮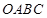 卷成一个以
卷成一个以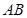 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长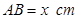 ,圆柱的体积为
,圆柱的体积为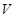
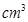 .
.
(1)写出体积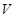 关于
关于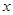 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当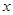 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积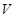 最大?最大体积是多少?
最大?最大体积是多少?
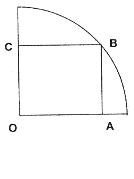
如图,在半径为
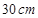 的
的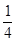 圆形(
圆形(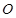 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料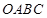 ,其中点
,其中点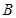 在圆上,点
在圆上,点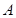 、
、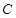 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮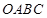 卷成一个以
卷成一个以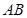 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长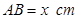 ,圆柱的体积为
,圆柱的体积为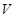
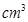 .
.
(1)写出体积
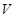 关于
关于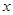 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;(2)当
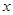 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积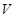 最大?最大体积是多少?
最大?最大体积是多少?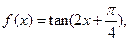 ,
,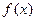 的定义域与最小正周期;
的定义域与最小正周期; ,若
,若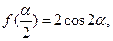 求
求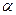 的大小.
的大小.